Стокесийн хоёрдугаар бодлого
Стокесийг таних байхаа. Навьер-Стокесийн тэгшитгэлийг үзэж байсан, физик дээр тунах бөмбөлөгний туршилт хийж байсан бол лавтай л сонсож байсан нэр байх. Стокес шингэний механикт маш олон зүйлийг судалж үлдээсэний хэсэг нь Стокесийн 1 ба 2-р бодлого, түүний шийдүүд юм. Энэ хоёр бодлогын шийд нь Навьер-Стокесийн тэгшитгэлийн одоогоор олдоод байгаа хэдхэн шийдний нэг юм. Сая долларын үнэтэй Навьер-Стокесийн тэгшитгэлийн шийд оршин байдаг гэсэн баталгааг саяхан Казакстаны эрдэмтэн 30 жилийн судалгааны үр дүнд гаргасан гэсэн боловч алдаа гаргасанаа хүлээн зөвшөөрсөнөөр түүний олон жилийн хөдөлмөр үгүй болсон юм. За энэ ч яахав Стокесийн 1-р бодлого гэж юу гэдгийг тайлбарлачихаад 2-луугаа оръё. Хязгааргүй үргэлжлэх хавтан дээр шингэн хөдөлгөөнгүй оршиж байна гэж үзнэ. Гэнэт уг хязгааргүй үргэлжлэх хавтан U гэсэн хурдтайгаар огцом хөдлөнө. Энэ үед шингэний хурдны профайлыг ямар байхыг бодож олохыг Стокесийн 1-р бодлого гэнэ.
 |
| Стокесийн хоёрдугаар бодлогын тооцонгийн шийд. |
Хоёрдугаар бодлого нь хоёр хязгааргүй үргэлжлэх хавтгайн дунд шингэн хөдөлгөөнгүй оршино гэж эхэлнэ. Харин хугацаа эхлэхэд доод эсвэл дээд хавтгайгын аль нэг нь синус эсвэл косинусын хуулиар хэлбэлзэн хөдөлж эхэлнэ. Хөдлөхдөө хязгааргүй үргэлжлэх чиглэлдээ нааш цааш болж хөдөлнө гэсэн үг. Уг хөдөлгөөнөөр шингэн ламинар урсгал бий болох ба уг усргалын хурдны аналитик шийдийг Стокес 1851 онд олсон учир түүний нэрээр Стокесийн 2-р бодлого гэж нэрлэгджээ. Зарим ном өгүүлэлд энэ бодлогыг хэлбэлзэх Чоуетте урсгал эсвэл Райлэйг-Стокесийн урсгал гэж бас нэрлэдэг. Энэ бодлогийг хэдүүлээ төгсөгөл ялгаварын /ТЯА/ болон сүлжээний Больцманы аргаар /СБА/ бодож үзье ээ. Бид аналитик шийд энэ тэрийг нь сонирхохгүй бөгөөд СБА ба ТЯА-уудыг хооронд нь харьцуулж үзэх гэж байгаа юм. Стокесийн 2-р бодлогын зургийг дараах зургаар харуулав.
 |
| Стокесийн хоёрдугаар бодлого. |
Эхлэхийн өмнө Навьер-Стокесийн тэгшитгэлийг хэвтээ чиглэлд /х-чиглэлд/ бичвэл
Дээрх зурагт үзүүлсэн урсгалын шинж чанар дээр үндэслэж дээрх тэгшитгэлийн хэвтээ чиглэл дахь дифференциалуудыг нь алгасаж болохоор байна. Яагаад гэвэл урсгал нь 1 хэмжээст бөгөөд у тэнхлэгийн дагуу л шингэний урсгалын өөрчлөлтийг олох хэрэгтэй болж байна. Ингээд у чиглэлд дахь дифференциал, хугацааны дифференциалтай хамт үлдэж тэгшитгэл
хэлбэртэй болох ба энэ тэгшитгэлийг Стокесийн 2-р бодлогын үндсэн тэгшитгэл гэнэ. Энд байх даралтын градиентыг алгасаж болно эсвэл ямар нэгэн тогтмол тоогоор авч болно. Яагаад гэсэн хоёр хавтгайн дунд оршин шингэн нь ямар нэгэн даралтанд оршиж байж болох юм. Тэгшитгэлд байх D нь зунгааралт бөгөөд тэгшитгэл 217-ын өөр нэг нэр нь адвекци-тархалтын тэгшитгэл учраас энэ нь тархалтын коэффициент байж болно. Энэ тэгшитгэлийг бодоход өгөгдөх анхны ба хязгаарын нөхцөл нь:
ба дээд хавтангийн хэлбэлзэх хурдыг
гэж өгье. Энд А нь далайц (м с-1) ,Т нь долгионы урт буюу үе (=5 sec), t нь хугацаа юм.
Энгийн Эйлэрийн арга /ТЯА/
Тэгшитгэл 217-ын хугацааны уламжлалд Эйлэрийн ялгавар, хоёрдугаар эрэмбийн дифференциалд төвийн ялгаварын схем зэргийг ашиглавал тэгшитгэл маань
болох ба энд u,n+1,j нь шинэ хугацааны алхам дахь j зангилаан дээрх хурд, delt t нь хугацааны алхам (=0.001 сек), delt y нь торны алхам (=0.2 m), D нь тархалтын коэффициент (=20 m2s-1), альфа нь тогтмолоор өгөгдөж буй даралтын утга зэрэг болно. .
Сүлжээний Больцманы арга
Нэг хэмжээст бодлогог учир бид D1Q3 гэсэн сүлжээг бодлогондоо ашиглана. Сүлжээний Больцманы аргад ямар нэгэн дифференциал тэгшитгэлийг тухайлбах, ойролцоолох гэдэг ойлголт байхгүй учираас тэгшитэл 217 - г бодлогод хэрэглэхгүй. Харин үүний оронд энэ тэгшитгэлийг төлөөлж чадахуйц сүлжээний Больцманы тэгшитгэлийг хэрэглэх ба энэ тэгшитгэл нь энгийн сүлжээний Больцманы тэгшитгэлтэй адил
гэж өгөгдөх ба f,n+1,i нь шинэ хугацааны алхам дахь j
нүдэн дээр байх i чиглэлд харах түгэлтийн функц, ciy нь y-тэнхлэгт чиглэх төгсгөлөг хурд, small delta t нь сүлжээний хугацааны алхам, wv нь тэнцвэрт орох параметр зэрэг болно. Энд байх сүлжээний хугацааны алхам нь бодлогын хугацааны алхамаас өөр бөгөөд ихэвчлэн үүнийг нэгж гэж авч үздэг. Сүлжээний алхамыг ч гэсэн нэгж гэж үзэж төгсгөлөг хурдны нэгж чанарыг хадгална. Харин тэнцвэрт түгэлтийн функц нь
гэж өгөгдөх ба энд байх u нь бидний мэдэхийг хүсэж буй хурд, wi нь сүлжээний жинлэх функц зэрэг болно. Сүлжээний тухайлсан төгсгөлөг хурд болон сүлжээний жинлэх функцын талаар өмнөх сүлжээний больцманы аргын тухай нийтлэлүүдээс олж авах боломжтой. Сүлжээний Больцманы тэгшитгэл нь СБА-ын алгоритмын дагуу урсах ба мөргөлдөх алхамуудаар шийдэгдэнэ. Харин тэнцвэрт орох параметр нь зунгааралттай холбогдох холбоогоор
гэж олдох боломжтой. Энд байх D нь нэгжтэй тархалт/зунгааралтын коэффициент, cs2 нь сүлжээний дууны хурд гэгддэг. Хугацааны алхам нь бодит хурдыг сүлжээний хурдруу шилжүүлэх масштаблалтаас
олдох боломжтой. Өөрөөр хэлбэл торны алхам, сүлжээний хурд хоёрыг сонгочиховол бодит хурднаас delta t -г дээрхээс олж болно. Бодит ба сүлжээний хурд гэдэг нь нэг нь нэгжтэй /м/с/ нөгөө нь нэгжгүй СБА-д ашиглагдах, бодогдох хурд юм. Өөрөөр хэлбэл СБА гэдэг нь нэгжгүй хэмжигдэхүүнүүд ашигдан тооцоо хийж нэгжгүй үр дүн гаргах учир түүнийг масштаблаж бодит хэмжигдэхүүн болгоно.
За ингээд сүлжээний хурдыг
гэж олох ба үүнийгээ тэгшитгэл 225-ын дагуу масштаблаж нэгжтэй хурд болгон авна.
Анхны нөхцөл, хязгаарын нөхцлийг доорхи кодонд харуулсан байгаа.
Харьцуулалт
Тооцоонд адилхан торны алхам, delt y=0.2 м авч үзэхэд ТЯА нь 0.001 гэсэн хугацааны алхам, СБА нь 0.01 гэсэн хугацааны алхамуудыг өгч байгаа юм. Энэ юу вэ гэхээр СБА зарим тохиолдолд тооцооллыг хурдан гүйцэтгэх боломжтой гэсэн үг юм. Ингээд тооцоог 20сек хугацаанд хийж үр дүнг харьцуулж харвал:
 |
| Стокесийн 2-р бодлогын үр дүн. Хэвтээ тэнхлэгт хугацаа, босоо тэнхлэгт у-тэнхлэг, өнгөтөөр ТЯА үр дүнг, Хар зураасаар СБА үр дүнг харуулав. |
Дээрх зургаас ялгааг олж харна гэдэг бэрх байна. Энэ нь хоёр арга маш ойролцоо үр дүнгүүдийг өгч байна гэсэн үг юм. Одоо кодны бүтцийг дараах хүснэгтээс авч үзье.
Хүснэгт. Стокесийн 2-р бодлогийг тооцон бодох Фортран кодуудын харьцуулалт
Төгсгөлөг Ялгаварын арга
|
Сүлжээний Больцманы арга
|
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
|
! initial conditions
do j=1,m
u(j) =0. ! zero clear
un(i)=0. ! zero clear
end do
! main loop
do n=1,nt !time starts
time=n*dt
! boundary condition
u(1 )=0.0
un(1)=0.0
u(m)=amp*sin(2.*pi*time/wp)
un(m)=u(m)
do j=2,m-1
rh=cc*(u(j+1)+u(j-1)-2.*u(j))+alfa*dt
un(j)=rh+u(j) ! next time
end do ! j
u=un ! for next time
end do ! time
|
!initial conditions
do j=1,m
u(j)=0.0
do k=0,2
f(k,j)=w(k)*u(j)
end do
end do
! main loop
do i=1,nt !time starts
! streaming
do j=m,1,-1
f(1,j)=f(1,j-1)
f(2,m-j)=f(2,m-j+1)
end do
! boundary condition
ul=amp_L*sin(2.0*pi*i/per_L)
f(2,m)=ul*(w(1)+w(2)+w(0))-f(1,m)-f(0,m)
f(1,1)=-f(2,1)
! macroscopic variable
do j=1,m
u(j)=f(1,j)+f(2,j)+f(0,j)
! collision
f(0,j)=(1.-ome)*f(0,j)+ome*w(0)*u(j)
f(1,j)=(1.-ome)*f(1,j)+ome*w(1)*u(j)
f(2,j)=(1.-ome)*f(2,j)+ome*w(2)*u(j)
end do
end do ! time
|
Дээрх кодонд харж байгаачлан СБА нь арай урт кодтой байна. Энэ нь тооцоог удаан хийнэ гэсэн үг биш боловч ямар нэгэн байдлаар нөлөөлнө. Яагаад урт байна вэ гэвэл гол тэгшитгэлийн тооцоо нь урсах ба мөргөлдөх алхам гээд хуваагдсан, дээрээс нь хурдыг олоод түүнийгээ масштаблах гэх мэт нэмэлт ажлууд байгаад байгаа. Дээрх хүснэгтэнд зөвхөн гол хугацааны гогцоог л харуулсан байгаа. Парамертрүүдийг оруулаагүй гэдгийг анхаараарай. Өөр нэг зүйл нь ТЯА-д тооцоог дор хаяж 3-н зангилаа ашиглаж хийж байгааг 20-р мөрнөөс харж болно. Гэтэл СБА-д дор хаяж 2 зангилаа ашиглаж байгааг 13 ба 14-ээс харж болно. Энэ нь ямар ач холбогдолтой вэ гэхээр СБА нь шууд зэрэгцээ тооцоолол хийхэд боломжтой, харин ТЯА нь шууд зэрэгцээлэх боломжгүй гэсэн үг юм. Тооцоонд ашиглаж байгаа зангилааны цогцыг тооцон бодох ухаанд шилбэ гэж нэрлэдэг. Энэ шилбэ олон зангилааг хамаарвал зэрэгцээ тооцоолол төвөгтэй, дан эсвэл хоёр зангилааг хамарч байвал зэрэгцээ тооцоолол амархан гэсэн үг юм. Ингээд буцаад үр дүнлүүгээ орвол
|
| Хурдны профайлын харьцуулалт. Улаанаар ТЯА, Хөхөөр СБА-ын үр дүнг харуулсан банйа. Сайн ажиглаж харвал доод хавтантай ойролцоо хоёр үр дүн жааран ялгарч гарч ирна. Энэ хоёр арга хоёулаа 2-р эрэмбийн нарийвчлалтай учир яг аль нь зөв бэ гэдгийг хэлэхэд бэрх. Үүнийг хэлэхийн тулд өндөр эрэмбийн арга эсвэл аналитик шийдний хариу хэрэгтэй. |
Нэг талаараа сүлжээний Больцманы арга давуу талтай, нөгөө талаараа дутагдалтай. Энэ нь тухайн бодлогоос хамаарна. Жишээ нь бидний энэ бодсон Стокесийн 2-р бодлогын хувьд бол СБА нь ТЯА-аас давуу байна гэж хэлж болохоор байна. Яагаад гэвэл том хугацааны алхамд хурдан тооцооллыг хийж сайн үр дүн өгч чадаж байгаа юм.
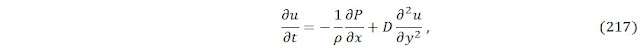
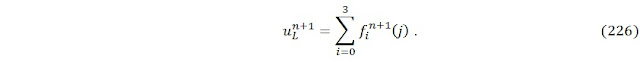
No comments:
Post a Comment