Үл шахагдах шингэний динамик дахь үндсэн тэгшитгэлийн тавилт /In-compressible flow governing equation with steady state convection diffusion equation/

Үл шахагдах шингэний динамик дахь Навьер-Стокес ба конвекци тархалтын тэгшитгэл, түүнийг хэрэглээ болох “Голын адаг дахь хагшаас болон давсны шаантагын харилцан үйлчлэл”ийн жишээн дээрх математик дүрслэл

Далайруу голын цутгах хэсгийг буюу голын төгсгөл хэсгийг голын адаг (estuary) гэж нэрлэнэ. Хагшаасны зөөгдөл элбэгтэй голын хувьд уг адаг хэсэгт голын ёроолын морфологийн онцлог хэлбэршилт бий болдог. Үүний шалтгаан нь далайн давстай усны нягтын түрлэгийн (densitycurrent) үзэгдэл болох давсны шаантаг (salt wedge) юм. Нягтаар хүнд давстай усны доогуур шургаж урсгалын эсрэг чиглэлд урсах ба нягтын тархалтын хэлбэр, түүний ерөнхий хөдөлгөөн нь мод материалыг зорох шаантаг лугаа ижил голын адаг орчмын ёроолын хэлбэрийг сөргүүлэн хэлбэршүүлдэг байна. Голын умбуур ба ёроолын хагшаас урсан далайд орж ирэхдээ уг шаантагны пронттой тулж улмаар босоо хөдөлгөөн нь идэвхижэн буцах хандлагатай болдог байна. Адаг орчмын далайн ихэнх боомтуудад умбуур ба ёроолын хагшаас, эсрэг урсгалтай давсны шаантаг нарын харилцан үйлчэлээр ёроолын хүйлс, атираашилт үүсэх нөхцөл бий болдог. Голын хагшаас, ууссан бодисын тээвэрлэлт, зөөгдөлт, далайн давсны тархалт, хагшаасны босолт гэх комплекс үэгдлийн математик загвар нь дараах байдлаар илэрхийлэгдэнэ.

Дээрх тэгшитгэл нь урсгал тасралтгүйн, Навьер-стокесийн, Конвекци-тархалтын тэгшитгэлүүд бөгөөд үүнд u_i, g, ro_w, ro’, delta, p, nu, D, c, u₁, u₂, w_s нар нь хурдны бүрдүүлэгч, хүндийн хүчний хурдатгал, жишиг нягт, харьцангуй нягт, дирак делта, даралт, зунгааралт, тархалтын коэффициент, концентраци, хэвтээ ба босоо хурднууд, тунах хурд, x_m, u_m, u₁, u₂, x₂, i=1, 2 зэрэг нь орон зайн дагавар тэмдэглэгээ, хурдны векторын дагавар тэмдэглэгээ, хэвтээ хурд, босоо хурд, босоо тэнхлэг, хэмжээсийн индекс зэрэг болно. Дээрх тэгшитгэлүүдийн математик дүрслэлийг хийж зарим гаргалгааг тодорхойлъё. 

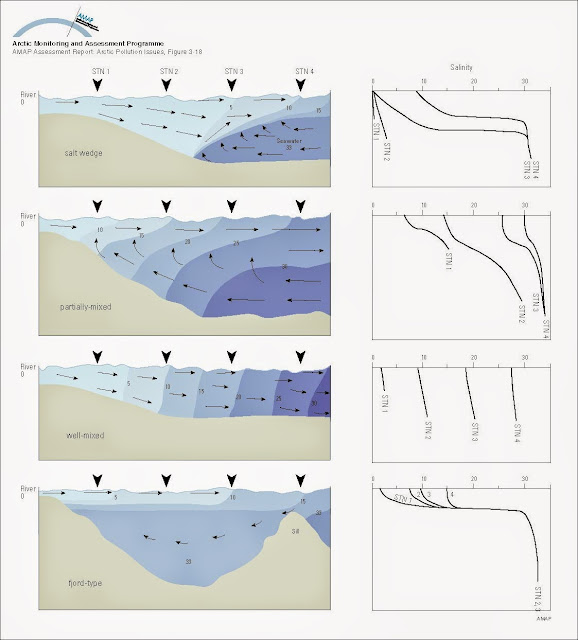
Figure 1. Давстай ус ба нягт багатай цэвэр устай холигдсон байдлаар нь ангилсан голын адгын төрлүүд. А-Давсны шаантагтай голын адаг, Б-хэсэгчлэн холилдсон голын адаг,В-Бүрэн холилдсон голын адаг, Г-Хашигдсан буюу сул холилдсон голын адаг. Эх үүсвэр http://www.amap.no/

Дээрхи дөрвөн төрлийн голын адгаас хамгийн элбэг тохиолддог төвөгтэй процессийн нэг нь давсны шаантаг юм. Давсны шаантагын урсгал болон давсны концентрацийн тархалт нь голын хагшаас, ууссан тээвэргэдэж тунасан бодисуудыг дахин хөдөлгөх хүчин зүйл болдог. Энэ үзэгдлийг Навьер-Стокесийн тэгшитгэлийг шууд тооцон бодох байдлаар тоон аргаар судлах боломжтой.

Үндсэн тэгшитгэлүүд /Governing equations/

Усны сан (water body) бүхий газрууд болох гол, нуур, далай гэх мэт дахь шингэний хөдөлгөөн нь бүгд үл шахагдах шингэний урсгалд хамрагдах учир урсгал тасралтгүйн тэгшитгэл дараах байдлаар бичигдэнэ.

Шингэний эгэл хэсэг дахь босоо ба хэвтээ хурдны векторуудын орон зайн өөрчлөлтийн нийлбэр нь 0 байвал үл шаагдах нөхцөл бүрэлдэнэ гэж үзнэ. Хурдын градиентийг гурван тэнхлэгт задалж бичвэл:

Дээрх томъёололд урсгал тасралтгүйн (нэг төрлийн масс хадгалагдах хууль-mass conservation law) тэгшитгэлийн гурван хэлбэрийг харуулж байна. Сүүлийн хэлбэрийг дагавар тэмдэглэгээг (suffix) ашиглан тэмдэглэсэн болно. Дагавар тэмдэглэгээ нь индексэн тэмдэглэгээтэй ижил боловч гол ялгаа нь нийлбэрээр задардагтай холбоотой юм. Дээрх сүүлийн тэгшитгэлийн i=1,2,3 гэсэн хэмжээсний тоо байх ба дагавар тэмлэглэгээ дараах байдлаар задарна.

Дагавар тэмдэглэгээг анх Эйнштэйн өөрийн ажилдаа хэрэглэж хэвшүүлсэн бөгөөд вектор ба матрицийг тэмдэглэхэд тохиромжтой, нийлбэр илэрхийллийг хураангуйлдаг учир нийлбэрийн журам (summation convention) гэж нэрлэгддэг. Шингэний динамикт бүхийл урсгал Навьер-Стокесийн тэгшитгэлд захирагдах ба уг моментийн (хөдөлгөөний тоо хэмжээ) тэгшитгэлийг ерөнхий хэлбэрээр хоёр хэмжээстэд бичвэл:

Дээрх тэгшитгэл дахь дөрвөлжин хаалтан доторхи зунгааралтын шүргэх хүчдэлийн гишүүнийг үл тооцвол Эйлерийн тэгшитгэл гарч ирнэ. Дээрх тэгшитгэлд гурав дахь багананд бичсэн орлуулгыг хялбарчилгааны үүднээс хийвэл дараах байдлаар бичигдэнэ.

Дээрх илэрхийллээс харахад эхний тэгшитгэлийн зүүн талд u1 ба u2 гэсэн адвекцийн илэрхийллүүд, хоёр дахь тэгшитгэлийн мөн илэрхийллүүд дагавар тэмдэглэгээгээд тэмдэглэгдэх боломжтой харагдаж байна.

Энэхүү тэмдэглэгээний шилжүүлгээс нийлбэрийн журам гэгдэх дагавар тэмдэглэгээний утгыг сайтар ойлгох боломжтой. Х ба У тэнхлэгийн дагуу бичигдсэн энэхүү хоёр илэрхийллийг нэг илэрхийллээр илэрхийлэх боломж харагдаж байна.

Дээрхтэй ижил байдлаар НСТ-ийн хурдны хугацааны өөрчлөлтийг нэгтгэн бичиж болно. Энэ нэгтгэл нь индекс тэмдэглэгээг ашиглаж байгаа юм.

Зунгааралтын илэрхийллийг дагавар тэмдэглэгээнд шилжүүлэх гэж оролдъё.

Мөн л хоёр тэнхлэг дээрх илэрхийллийг нэг тэнхлэгт индекс тэмдэглэгээ ашиглан шилжүүлэх боломж харагдаж байна. Иймд зунгааралтын илэрхийллийг бүрэн байдлаар бичвэл:

Ингээд НСТ-ийг нэг хураангуй хэлбэрт оруулан бичих боломж олдож байна. Даралтын орон зайн өөрчлөлтийг мөн индекс тэмдэглэгээгээр дээрхүүдтэй ижил байдлаар хураангуйлна. Тэгшитгэлийг товч бөгөөд хураангуй харуулах нь шингэний динамикт асар ач холбогдолтой байдаг. Бүрэн тэгшитгэлүүд ихэвчлэн гурван тэнхлэгт ижил задарч, шугаман бус, вектор, тенсор (заримдаа тензор) илэрхийллүүдийг агуулдаг учир хураангуйлан харуулах нь илүү ойлгомжтой болгодог.

Энэ нь 2 хэмжээст орчин дахь Навиер-Стокесийн тэгшитгэлийн ерөнхий хэлбэр юм. Уг тэгшитгэлд байгаа Диракделта функц нь хэвтээ тэнхлэгийн дагууд хүндийн хүчний хурдатгалыг тэглэх үүрэгтэй орно. Делта функцийн утга нь дараах байдлаар илэрхийлэгдэнэ.

Давс болон хагшаасны хөдөлгөөн конвекци-тархарлтын тэгшитгэлээр тодорхойлогдоно. Иймд конвекци-тархалтын тэгшитгэлийг Фикийн 1-рхууль дээр үндэслэн тодорхойлъё.

Конвекци-Тархалтын тэгшитгэл (Convection-diffusion equation)

Адвекц ба конвекцийн ялгааг төдийлөн гаргаж чадахгүй байгаагийн уршигаар уг хоёр үгийг монгол дээр буулгахад бэрх байгаа юм. Энгийн хэлэнд уг хоёр үг ойролцоо утгатай үг боловч зарим шинжлэх ухаанд огт ялгаатай утгыг илэрхийлнэ. Ус цаг уурын хувьд конвекцийг түлхүү хэрэглэх ба тэнд адвекцийн үзэгдэл байдаггүй гэж үздэг нь конвекци нь температур дулаантай холбоотой гэдгийг илтгэнэ. Техникийн хэлэнд конвекцийг тархалт ба адвекцийн нэгдлээр илрэх үзэгдэл хэмээн дүгнэсэн байдаг. Тархалт гэдэг нь ямар нэгэн бодисийн концентраци шингэн дотор тарж тэнвэрт байдалруу тэмүүлэх үзэгдлийг хэлдэг бол адвекц гэдэг нь ууссан бодис эсвэл умбуур матери нь концентраци тоо хэмжээний шинж чанараа хадгалж шингэнээр үйлчлүүлэн шилжэх үзэгдлийг хэлнэ. Зарим практикт шингэний температурын нөлөөллөөр хөдөлгөөнд орохыг конвекци, ууссан бодис элдэв зүйл урсгалаар зөөгдөхийг адвекци, уг элдэв материйн концентраци өөрчлөгдөхийг тархалт буюу диффузи гэнэ гэж тайлбарладаг. Шингэний динамикт ерөнхий тохиолдолд адвекцийг конвекци хэмээн хэрэглэнэ. Конвекци-тархалтын тэгшитгэлийг тодорхойлохын тулд шингэний өчүүхэн эгэл хэсгийг сонгон түүнд орох ба гарах цулхэлтийн (flux) балансийг авч үзье.

Figure 2. Хоёр хэмжээст шингэний элементар хэсэг ба түүнд орж гарах цүлхэлтүүд

Дээрх зурагт хоёр хэмжээст шингэний элементэр хэсэгт орох концентрацийг хөх сумаар, гарах концентрацийг улаан шугамаар тэмдэглэв. Шингэний тогтворжсон (steady state) урсгалын нөхцөлд бодисын концентрацийн гарах цүлхэлтийг Фикийн нэгдүгээр хуулиар илэрхийлж болно.

Наблагийн (Гамельтон, дуудахдаа del гэнэ.) оператор Del нь градиентийг тэмдэглэх ба дараах байдлаар илэрхийлэгдэнэ.

Фикийн хуулиар бусад физик хэмжигдэхүүнүүдийн цүлхэлтийг тодорхойлж дараах хүснэгтээр харуулъя (Stocker, 2011).

Харин авч үзэж буй элементар хэсгийн хувьд балансийн тэгшитгэлийг ойролцоолж бичвэл:

Хэвтээ тэнхлэг дахь цүлхэлтийн ялгаварыг элементар хэсгийн төв орчимд Тэйлорын цуваанд задалж тодорхойлж болно.

Үүнтэй ижил байдлаар босоо тэнхлэг дахь цүлхэлтийн ялгаварыг төв орчимд Тэйлорын цуваагаар тодорхойлбол:

Задаргаа 15 ба 16 – г тэгшитгэл 14-д орлуулан бичвэл:

Тэгшитгэл 17 нь хоёр хэмжээст тархалтын тэгшитгэл бөгөөд үүнд байх F_x, F_y – ийн оронд Фикийн тархалтын утга тэгшитгэл (13)-ийг орлуулбал:

Тэгшитгэлийг индекс тэмдэглэгээгээр хураангуйлан бичсэн болно. Энэ тэгшитгэл нь конвекцигүй дан тархалтын тэгшитгэлийг харуулна. Конвекцийн тэгшитгэлийг мөн хоёр хэмжээст элементар хэсэгт гарган авъя. Элементар хэсэгт орж байгаа болон гарч байгаа ууссан бодисын цүлхэлт нь концентрацийг талбайгаар үржүүлсэнтэй (хэвтээ чиглэлд delta c* delta y гэх мэт) тэнцүү байна. Тодорхой хугацааны delta t агшины дараах цүлхэлтийн утга, хугацааны өмнөх цүлхэлтийн утгатай тэнцүү байх нь конвекци буюу адвекци зөөгдөлтийн чанар юм.

Figure 3. Ууссан бодисын концентрацийн зөөгдөлт, элементар хэсгийн цүлхэлтийн оролт гаралт

Дээрх зөөгдөлтийн нөхцөл ёсоор орж байгаа бүх цүлхэлтийн нийлбэр гарч байгаа бүх цүлхэлтийн нийлбэртэй тэнцүү байх ёстойг бичвэл:

Концентраци ба орон зайн хэмжигдэхүүнүүдийг тэгрүү тэмүүлсэн хязгаар авч дагавар тэмдэглэгээгээр тэмдэглэвэл:

Концентраци нь скаляр хэмжигдэхүүнтэй агаар нэг ба үүний оронд нягт, даралт мөн байж болно. Тэгшитгэл 20-ийг заримдаа моментийн зөөгдөлт гэж нэрлэх тал бий.

Одоо конвекци тархалтын тэгшитгэлийг хагшаасны концентрацийн хувьд тэгшитгэл 18 ба 20 – ийн тусламжтайгаар угсарвал:

Хагшаас нь урсгалын дагууд ширхэглэлүүд нь хүндийн жингээрээ тунах болно. Тунах хурд нь босоо чиглэлтэй байх учир конвекцийн гишүүн задарч бичигдэхээс өөр арга байхгүй.

Энд dablu_s нь ширхэглэлийн (particle) тунах хурд (settling velocity) бөгөөд Наблагийн квадрат нь Лапласын оператор (Laplace operator) болох ба энэ нь градиентад дахин вектор оронгоор (дивергенц) үйлчилсэнийг илэрхийлнэ. Дивергенц (divergence) нь нэгэн төрлийн скаляр үржвэр (dot product) бөгөөд дараах байдлаар илэрхийлнэ.

Харин нягтын үйлчлэл ба тархалт шилжилтийн хувьд тэгшитгэл 21-ийг сийрүүлж бичвэл:

Хагшаас ба нягтын үйлчлэлийн хувьд бичигдсэн конвекци тархалтын тэгшитгэл дахь тархалтын коэффициент D нь тул бүрээс хамаарч өөр байх ба туршилтад тулгуурлан гаргаж авна.

Буссенискийн ойролцоолол (Boussinesq approximation)

Шингэний динамикт байгалийн конвекци бүхий урсгалд ихэвчлэн Буссенискийн ойролцооллыг хэрэглэдэг. Дэлхий дээрх ихэнх усны санд температур болон нягтын өөрчлөлт маш бага байх ба температурын градиентаас үүдэлтэй эзлэхүүний тэлэлт бас л харьцангуй бага байна. Иймд өчүүхэн бага байх өөрчлөлт пульсацыг тооцоонд оруулахгүй орхигдуулахад онцын ялгаа үүсдэггүй. Гэвч нягтын өөрчлөлт нь хүндийн хүчний хурдатгалд чухал нөлөө үзүүлэх учир уг илэрхийлэл дахь өөрчлөлтийг тооцоонд авч үзэхийг Буссенискийн ойролцоолол гэж нэрлэнэ. Шингэний нягтыг пульсацын хамт илэрхийлбэл:

Энд ро_w нь усны нягт ба үүнийг жишиг утга (reference value) хэмээн үзнэ. Тэгшитгэл 11-ийг гурван хэмжээст болгож нягтаар үржүүлэн бичвэл:

Буссенискийн ойролцоололийг хийхийн өмнө Навьер-Стокесийн тэгшитгэл Нюьтоны хоёрдугаар хууль болохыг харахад тэгшитгэл 26-ийн хэлбэр хамгийн тохиромжтой. Нягт гэдэг нь шингэний масс ба эзлэхүүнээс хамаарна. Нягтын оронд үүнийг орлуулж эзлэхүүнийг тэгшитгэлийн хоёр талаас хасвал ерөнхий хэлбэрийг олох болно. Тэгшитгэлийн зүүн талын хурдны өөрчлөл ба моментийн зөөгдөлт нар нь хурдатгал бөгөөд тэгшитгэлийн баруун талын илэрхийллүүд тус бүр хүндийн хүч, даралтын хүч, зунгааралтын хүчийг илэрхийлнэ.

Харьцангуйн ерөнхий онолыг бодвол Нюьтоны 2-р хууль хөдөлгөөний ерөнхий тогтолцоог дэлхий дээрх үзэгдэлд хангаж чаддаг нь шингэний динамикт ийнхүү илэрдэг. 

Тэгшитгэл 26-ийн хүндийн хүчний хурдатгалтай хэсэгт нягтын өөрчлөлтийг тооцох нь Буссенискийн гол санаачлага бөгөөд эл ёсоор тэгшитгэлд томъёо 25-ийг орлуулбал:

Ойролцоолол ёсоор бусад бүх нягтуудын пульсацыг тооцохгүй учир жишиг утга ёсоор усны нягтаар бичив. Буцаж тэгшитгэлийн үндсэн хэлбэрт оруулахын тулд гишүүд бүрийн усны нягтад хуваавал Буссенискийн ойролцоолол бүхий НС-ийн тэгшитгэл гарна.

Голын адаг дахь хагшаас ба давсны шаантагийн харилцан үйлчлэлийг дээрхээр гаргалгаа хийсэн гурван тэгшитгэлийн хослолоор шийдвэрлэнэ.

Уламжлалт арга болох төгсгөлөг аргаар тооцон бодох боловсруулалтыг загварчлалыг үйлдсэн багшаасаа зөвшөөрөл авч оруулах болно. Уг тэгшитгэлийг ТЯ-ын 1-р эрэмбийн эсрэг схем болон төвийн ялгатарын схемын хослолыг ашиглан даралтын аргын тогтворшилтын нөхцлөөр итерацилсан кодыг зохиогч бол Профессор Хосояамада Токузо юм.