Геофизик урсгал дахь хагшаасны динамикийн хоёр фазат загварчлал дээрх 3-р бага хурлын тойм
 |
| THESIS-2016 хуралд ханын илтгэл тавьж байгаа нь. |
Товчхондоо энэ хурал нь хагшаасны динамик, зөөгдөлтийн тухай загварчлал дээр төвлөрсөн дэлхийн шилдэг, тэргүүлэх судлаачдын цуглаан гэж хэлж болно. Энэ хуралд оролцож олон шинэ соргог, мэдлэгийг сонсож авсандаа баяртай байгаа бөгөөд хурлын дундуур тэмдэглэж авсан тэмдэглэлээсээ энд хуваалцая.
Энэ удаагын хурлыг Японы Чуо их сургууль 2016 оны 9 сарын 12-14 - ний хооронд зохион байгуулсан юм. Энэ хуралд багш Хосояамада Токузо, хамтрагч Отаке Такешигийн хамт "Окозү сувгийн аман дахь хагшаасны зарцуулгын загварчлал" хэмээх ханын илтгэлийг хэлэлцүүлэхээр оролцсон юм. Илтгэлийг энд дарж үзэж болно.
Ханын илтгэлийг зураг байдлаар харуулъя.
 |
| Ханын илтгэлийг pdf -ээр эндээс татаж авч болно. Ханын илтгэл А0 цаасан дээр бэлдэх гэж байгаа хүмүүс эндээс загварын санаагаа авч болно. Хагшаас шороо гэдэг бол бор өнгөөр илэрхийлэгдэх учир ерөнхий чимэглэлийг бор өнгөөр сонгосон болно. |
Ханын илтгэлийн үеэрх фотонууд: Гурван зохиогч
 |
| Проф. Хосояамада Токузо түүний чиглэл нэгт судлаачидад хийсэн ажлынхаа талаар тайлбарлаж байна. Эдгээр хоёр судлаач нь 1000 инженерийн төсөлд хамрагдаж байгаа консерциум их сургуулийн профессорууд гэсэн. |
 |
| Отаке Такеши - магист оюутан байхдаа энэхүү загварчлалын ажилд гар бие оролцож магистрын ажлаа хагшаасны гурван хэмжээст загварчлалаар хамгаалсан юм. Одоо Японы томоохон ЭКОХ хэмээх зөвлөх компанид ажиллаж байгаа. Фортран, С++, С зэрэг хэлнүүдийн өндөр мэдлэгтэй залуу байна. Хурлын үеэр ирж дэмжсэн юм. |
 |
| Япон тэнгис дагуух далайн эрэг угаагдал ихтэй байдаг бол бидний судалгааны обьект Окозу сувгийн адаг дахь эрэг эсрэгээрээ далайруугаа тэлээд байгаа юм. Энэ нь голын хагшаасны зөөгдөлт их байгаатай холбоотой бөгөөд энэ үзэгдлийг судлан загварчилж тооцоолсон юм. |
За ингээд үндсэн ажил болох хурлын тоймруугаа оръё. Авагдсан зураг болгон шинэ санааг илтгэх байх гэж найдаж байна.
Tatsuhiro Uchida - хурлын дарга хурлыг нээж байна.
Хурлын нээлтийн үг
Проф.
Тацухико Үчида – Хиймэл оюун ухаанаар мэргэшсэн.
Шингэний динамик
болон хагшаасны тооцооллын тухай энэ хурал инженерчлэл болон академик мэдлэгт ямар
нэгэн хувь нэмэр оруулна гэж бодож байгаа тухайгаа дурьдсан юм.
Хоёр дахь
нээлтийн үг.
Проф Тошиказү Като. Чуо их сургуулийн проректор.
Хоёр фазат
загварчлал нь маш итгэл төрүүлж байгаа аргачлал юм. Энэ хурал нь судалгааны
хөгжилд их ач холбогдол өгч байгаа бөгөөд сэдвийн хүрээнд маш их өндөр чанар
бүхий эрдэм шинжилгээний ажил хэвлэгдэж байна. Саяхан цунами болон тайфунаар
олон газар хохирол амссан бөгөөд эдгээр асуудал нь хагшаас болон хатуу урсацтай
маш нягт холбоотой байгаа учир ач холбогдолтой сэдэв юм. 52 хураангуй хүлээн
авч хянан шинжилгээ хийсний эцэст 46 дэлгэрэнгүй хураангуй болон урилгаар
хэлэлцүүлэх илтгэлийн хураангуйг хурлын эмхэтгэлд хэвлэсэн байгаа. Бүх
хэвлэгдэж хэлэлцүүлэгдэж байгаа өгүүллүүд маш өндөр чанартай гэдгийг хэлэхэд
итгэлтэй байна. Бидэнд зэрэгцээ хурал байхгүй учир бүх хүнд бүх илтгэлүүд
хүрэлцэж хэлэлцэгдэнэ гэж найдаж байна. Маргааш буюу хурлын хоёр дахь өдөр
тусгай хэлэлцүүлэг сургалт байгаа. Түүнд хагшаасны загварчлалын шинэ арга
аргачлалуудыг хэлэлцэнэ. Урилгатай зочидууд болон илтгэл хэлэлцүүлэх, сонсох оролцогчид
санаа, мэдлэгээ хуваалцана гэж бодож байна. Баярлалаа.
Хаав.
Урилгаар тавигдаж буй лекцүүд.
Тооцон бодох
хагшаасны динамик дахь нарийвчлал өндөртэй эгэл хэсгийн арга.
Хитоши Гото-Кёото
их сургууль
Далайн эргийн
инженерчлэлийн профессор. – Өндөр бүтээмжтэй тооцоолол хийдэг, хоёр фазат
урсгалыг эгэл хэсгийн аргаар тооцоолдог. Уулын гол, догшин урсгал дахь
хагшаасны зөөгдөлтийг тооцоолдог.
Уулын голд бид догшин
усргалыг олж харна. Энд хүндийн хүч зонхилох байр суурьтай байх ба гол
нөлөөлөгч хүч юм. Маш өндөр концентарицтай хагшаас зөөгдөж байдаг. Хоёр төрлийн
чөлөөт гадаргууг ойролцоолох аргаас бүрэн чөлөөт хэлхээсгүй аргыг авч үзнэ.
Эгэл хэсгийн аргад гөлгөржүүлсэн болон хөдөлж буй хэсгийн хагас илэрхий аргууд
хамаарна. 1996 онд Кошизука нараар хөдөлж буй эгэл хэсгийн хагас илэрхий арга (MPS-ХЭХИ)
зохиогдсон. Гөлгөржүүлсэн Эгэл хэсгийн Гидродинамикийн арга нь илэрхий арга
бөгөөд зарим тохиолдолд хагас илэрхий болдог байхад ХЭХИ арга нь хагас илэрхий
нь давамгайлж байдаг. Хагас илэрхий алгоритм нь илэрхий тооцоолол ба далд
тооцоолол гэсэн хоёр алхамаар хийгдэнэ. Хоёр дахь алхамд даралтыг шийдвэрлэдэг.
Давалгаа ханан дээгүүр давах лабораторын туршилтыг хийж ХЭХИ аргаар тооцоо хийж
зарцуулгуудыг харьцуулсан байна. ШЭАрга нь маш бага зарцуулгыг харуулж байсан
нь шингэний адвекцитай болон догшин урсгалтай холбоотой юм.
Эгэл хэсгийн
аргад нэг дутагдал байгаа нь даралтын асуудал юм. Гидростатик нөхцөл бүрэлдэхэд
төвөгтэй, даралт үргэлж савалж байдаг байна. Иймд маш нарийвчлалтай эгэл
хэсгийн аргыг боловсруулсан байна. Энэ арга нь эерэг даралтыг бий болгох хэд
хэдэн схемүүдээс бүтнэ. CMPS загварт даралтын градиентын загварыг оруулж өгч
түүн дээр тэгш хэмийг хангах засвар хийж өгсөн байна. Стандарт ХЭХИ аргад
Лапласыг хэрэглэдэг бол Поссионы тэгшитгэлийг хэрэглэх боломжтой. Үүн дээр
тусгалын аргыг хэрэглэж өөр нэг даралтын градиентын схемийг гаргаж ирнэ. Үүнийг
ECS схем гэнэ. Шууд Поссионы тэгшитгэлийг хэрэглэвэл HS гэсэн схем гарч ирнэ. Боловсруулсан
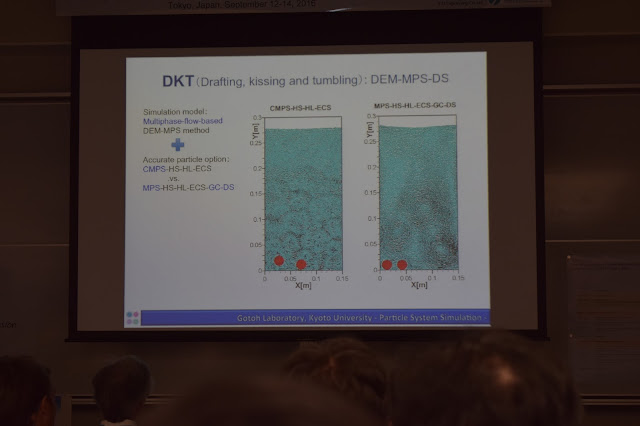
схемүүдээ хослуулан даралтыг усан баганын задрал дээр туршиж үзсэн байна. CMPS-HS-HL-ECS
хэрэглэхэд даралтын савалгаа байхгүй болж нарийвчлал өндөрссөн байна. Энэ
схемээ мулти-физиктэй холбоотой аргад хэрэглэж эхэлсэн байна. Шингэн-байгууламж-хагшаасны
харилцан үйлчлэлийн тооцооллыг давалгаа таслагч барилга дээр авч үзсэн байна.
Түүнийгээ ажиглалтын зурагтай харьцуулж баталгаажуулсан байна. Нөгөө талаас эерэг
даралтын үед дээрх схемүүд болох боловч сөрөг даралтын хувьд сайжруулалт
хийгдэх хэрэгтэй болно. Энд градиентын сайжруулалтыг хийнэ. Лапласд Тэйлорын
цуваа хэрэглэж интерполяцаар үржиж тенсор үржвэр аваад градиентын засвар гарах
нь. Үүнийг GC схем гэж нэрлэнэ.
Хоёр шинэ зүйлийг
танилцуулъя. Хуурмаг зунгааралт гэдэг зүйл байдаг. Үүнийг яаж багасгах вэ гэдэг
нь асуудал юм. Энэ нь чөлөөт гадаргуугын хязгаарын нөхцөлтэй холбогддог.
Даралтын градиентын математик загвар нь эгэл хэсэг хоорондын түлхэх хүчийг бий
болгодог. Энэ нь тооцооллын тогтворгүйжилтийг бий болгоно. Засварласан ХЭХИ
аргад хуурмаг түлхэхлцэх хүчийг нэмж өгсөн. Хоёр фазат тооцооллыг хийж өгсөн
байна. Үүгээрээ хурдны савалгааг судалж сайжруулалт хэрхэн ажиллаж байгааг
судалжээ. Хоёр фазат тооцоололд градиентын засвар маш чухал үүрэгтэйг дагах,
мөргөх, суух (DKT) бодлого дээр үзүүлсэн байна.
Усны чөлөөт
гадаргуугын нөхцөл нь нэг чухал бөгөөд төвөгтэй хэсэг. Энд орон зайн потенциал
эгэл хэсгүүдийг хэрэглэсэнээр тооцооллын нарийчлал сайжрана. Энэ нь хоосон орон
зайг илэрхийлэх нэг эгэл хэсгийг нэмсэнээр шийдэгдэнэ. Үүнийгээ хэрхэн
ажиллахын шалгахын тулд квадратад байгаа шингэнийг төвийг нь тойруулан
эргүүлэхэд төвд хоосон орон зай үүсвэл загвар муу ажиллаж байна гэж үзнэ. Мөн
саад тойрох урсгалыг бодож шалгасан байна. Өнөөдөр та бүхэнд засваруудыг танилцууллаа. Нэмэлт хоёр
сайжруулалтыг мөн танилцуулж байна. Дууслаа.
Асуулт: Энерги
хадаглагдах талыг асуув. – Энерги хадгалалтыг сайжруулах талаар ажиллаж байгаа.
Кинетик энерги алдагддаж байгаа нь зарим бодлого дээр ажиглагддаг.
Асуулт: Эдгээр
сайжруулалтуудыг ГЭГ-д ашиглаж болох эсэхийг асуулаа. Хамгийн гол нь илэрхий
эсвэл далд схем гэдгийг анхаарах хэрэгтэй. Хоёр арга хоёулаа хуурмаг даралт,
зунгааралтын асуудалтай байдаг.
Асуулт: Яаж
тусгаарлагдсан эгэл хэсгийг тодруулах вэ? - Энд бид эгэл хэсгийн дугааруудыг
хэрэглэнэ. Үүгээрээ аль эгэл хэсгүүд тусгарлагдсан бэ гэдгийг тодорхойлно. Том
хуйлралтын загварчлалыг эгэл хэсгийн аргаар тооцох гэж оролдож байгаа ч сайн үр
дүн гарахгүй байна.
1–р
хэсэг, үндсэн илтгэлүүд
Хатуу урсацын Эйлэр-Лагранжийн тооцоолол
Фукуда
Тооцооллын арга, баталгаажуулалт, жишээ бодлогууд, хоёр фазат тооцоололын
тухай ярьна. Эйлэр-Лагранжийн арга нь шингэн ба эгэл хэсгийн харилцан үйлчлэлд
чухал үүрэг гүйцэтгэж ирсэн. Маш өндөр концентрацитай хатуу урсацыг
загварчлахад тохиромжтой. Лабораторын туршилт мөн гүйцэтгэсэн байна. Шингэний
урсгалыг Эйлэрийн торон дээр тооцож эгэл хэсгүүдийг бөөгнөрсөн бөмбөлөгөөр
бүтээж Лагранжийн аргаар тооцно. Харилцан үйлчлэлийн хүчийг Салангид элементийн
аргаар тооцсон байна. Үелэх хязгаарын нөхцлийг өгч жинхэнэ голын хайрганы
зөөгдөлтийг тооцоолсон байна. Концентраци 0.44 байх үед хайрганы хувилбар нь
маш удаан зөөгдөлттэй байсан байна. Урсгалын хурдны босоо хуваарилалтыг хэмжиж
туршилттай харьцуулсан байна. Мөн концентрацийг харьцуулж үзсэн байна.
Хоёр фазат урсгалд шингэн ба хатуу эгэл хэсэг дээрх хүчдэлүүдийг бодож
үзсэн байна. Хагшаасны концентраци ихэсвэл харагдах үрэлтийн өнцөг нь ихэсдэг
байна. Оновчтой хагшаасны мөхлөгийн хэлбэрийг сонгосоноор хагшаасны зөөгдөлтийг
нарийн тодорхойлж болохоор байна.
Асуулт: Эгэл хэсгүүдийг харилцан үйлчлэлийн загварын тухай асуув. – Уян
харимхайн хүч, Бууруулах коэф, үрэлтийн хүч гэх мэтийг авч үзсэн байна.
Асуулт: Туршилтанд жинхэнэ голын хайргыг ашигласан уу. – Туршилт болон
тооцоолол хоёрт авч үзэж буй эгэл хэсгүүдийн хэлбэр ижил байх ёстой. Туршилтаас
санаандгүй түгэлтийг авч үзэж дундаж хэлбэрээр тооцооллыг үйлдэх хэрэгтэй гэсэн
санал хариултнаас урган гарав.
Асуулт: Тооцооллын хугацааны тухай. 1 Секундын үзэгдлийг 3 хоногт тооцоолох
хэмжээний хугацаа зарцуулдаг байна.
Гурван хэмжээст хатуу урсацыг Салангид Элемент-ХЭХИ хосолцсон аргаар
тооцсон нь.
Цурута
Гол санаа нь уулын голын гэнэтийн үер юм байна. Маш их хөрс чулуулагаар
дүүрсэн урсгалыг загварчлах нь гол зорилго нь байна.
Энд догшин урсгал, хатуу хэсгүүдийн харилцан үйлчлэл, хатуу шингэний
харилцан үйлчлэл зэргийг авч үзэх хэрэгтэй. Хэлхээст суурилсан арга нь маш том
хэв гажилтыг гаргахад хэцүү учир чөлөөт аргыг хэрэглэж байна. Хатуу хэсгүүдийн
хоорондох харилцан үйлчлэлийг Салангид элементийн аргаар тооцох боломжтой
байна. Хөдлөх хэсгийн хагас илэрхий аргын талаар тайлбарлаж шингэний ба хатуу
хэсгийн харилцан үйлчлэлийн нарийвчлалын талаар ярив. Тухайлбал хэт ойрхон хоёр
хатуу хэсгийн голоор шингэний эгэл хэсгүүд орохгүй байхгүй байх нь нарийвчлалыг
бууруулна. Үүнийг сайжруулсан байна. Энэ сайжруулалтанд хоёр өөр түвшний
тухайлсан оронг хэрэглэнэ. Нэг нь шингэнд нөгөө нь хатуу хэсэгт хамаарах ба
тэдгээрийн тусгал дээр харилцан үйлчлэлийг тооцоолно. Алгоримт нь шулуун
хэлбэртэй тасралтгуйн болон момент хадгалагдах тэгшитгэлүүд шингэн ба хатуу
хэсгүүдэд үйлчилнэ. Туршилтыг дотроо савхнуудтай усан баганын задралаар үйлсэн
байна. Ханын хязгаарын нөхцөлд ханын потенциал эгэл хэсгийг ашигласан байна. Үүнийг
ашиглахад авч үзэх эгэл хэсгүүдийн тоо буурдаг байх нь. Мөн эгэл хэсгүүдийг
хайх хугацаа багасдаг байна. Жишиг бодлогуудыг шингэн шингэн болон хатуу хатуу,
шингэн хатуу гэсэн байдлаар авч үзсэн байна. Ханын барзгар нь тохируулж өгсөн
эгэл хэсгүүдээс хамаарна.
Аналитик аргатай харьцуулсан ба зарим нэг хатуу болон шингэний эгэл хэсгүүд
аналитик шийднээс илүү гарсан байна. Хана болон сувгийн ёроолд ирэх хүчийг
тооцоолж онолтой харьцуулсан байна. Хананд нэмсэн нэмэлт эгэл хэсэг нь
тооцооллыг нарийн болгож хүчийг зөв тооцоолоход нөлөөлдөг байна.
Асуулт: Хэт их концентрацитай үед шингэний урсгалыг хэрхэн нарийвчлалтай
тооцох вэ? Яваандаа сайжруулах болно.
Асуулт: Тосолгооны хүчийг тооцож үзсэн үү. Хараахан тооцож үзээгүй
бололтой.
Салангид элементийн аргын хэрэглээ, хатуу урсац
Харада
ХЭХИ арга болон СЭА нарын хослолын тухай илтгэнэ. Swashing sediment.
Далайн эрэг, давалгаа, элсний зөөгдөлт зэрэг нь төвөгтэй хязгаарын нөхцөл
бүхий урсгалыг бий болгодог. Одоогоор загварчлал маш ховор байгаа учир шинэ
тооцооллын аргачлал боловсруулав. Энэ арга нь догшин урсгалыг, ёроолын
өөрчлөлттэй хамт тооцохоос гадна шүүрэлтийг мөн тооцно. Шингэний болон хатуу
хэсгийн хамаарлыг харилцан үйлчлэлийн хүчээр тооцож өгнө.
Энэ хүч нь
шингэнд болон хатуу хэсэгт өөр байдлаар тодорхойлогдоно. Гэхдээ энэ нь момент
хадгалдаггүй ба ирээдүйд сайжруулна гэнэ. Далайн эргийн давалгааны тооцоог хийсэн
байна. 6 удаагын давалгаа цохиход хөрсний бүрэлдэхүүн өөрчлөгдсөн байна.
Бүрэлдэхүүндээ хайрга болон пластик бөмбөлөгийг авч үзсэн байна. Шиэлдсийн тоо
болон засварласан Шиэлдсийн тоо зэргийг шүүрэлтийн урсгалд авч үзсэн байна. Тооцооллын
үед давалгааны өндөр болон хурднаас болж хөрсрүү шингэх усны шингэлт их байгааг
харуулсан байна. Хагшаасны зөөгдөлтийг тооцохдоо шүүрэлтийн нөлөөллийг тооцох
хэрэгтэй гэдгийг харуулж байгаа юм байна. Санал болгож байгаа загвар нь момент
хадгалагдахгүй байгаа нь нэг сул тал байна.
Асуулт: Харилцан
үйлчлэлд яагаад хоёр өөр хүчийг хэрэглэж байгаа юм бэ. Ерөнхийдөө өгүүллүүдээс
санаа авсанаа хэлэв. Янз бүрийн туршилтууд хийгээд өөр өөр хүчний томъёолол
ашиглах нь тохиромжтойг олж мэдсэн боловч момент хадгалагдахгүй байгааг
илрүүлсэн. Энэ дээр ажилахаар болж байгаа юм байна.
Асуулт: Шүүрэлтийн
нөлөөлөл хэр нөлөөлөхийг дэлгэрүүлж өгнө үү. Хагшаас босоод буцаад буух гэх мэт
нь тооцоололд харагдахгүй байна. --- Бид маш том хэмжээтэй хагшаас авч үзэж
байгаа учир хагшаас босолт харагдахгүй байгаа юм. Зөвхөн өнхрөх үзэгдэл
ажиглагдана.
Сэтгэгдэл: Тооцоонд
ёроолын хөрсний эгэл хэсгүүд давалгаа буцсаны араас сорогдож байгаа мэт харагдаж
байна. Энэ нь эргийн элэгдэлд маш чухал үзэгдэл учир сонирхолтой санагдлаа.
Асуулт: Үндсэн
тэгшитгэлүүдийг харуулахгүй юу? Хөвөлтийн хүчийг яаж тооцсон бэ? Хөвөлт нь
турбулент урсгалд бараг тооцоолох шаардлагагүй боловуу гэж үзэж байна. – Хөвөлтийг
тооцоход хүрээлсэн хангалттай хэмжээний эгэл хэсгүүд байх хэрэгтэй. Энэ удаад
бага нарийвчлалтай тооцооллыг хийж байгаа учир хөвөлт нарийн тооцогдоогүй.
Тоорман
Шаварлаг
хагшаасны барьцалдалт болон түүнийг ойролцоох 1 хэмжээст босоо өөрчлөлтийн
аргын хэрэглээ.
Донг
Хэрхэн
хугацаанаас хамаарсан барьцалдалт бий болох вэ? Үүнд концентраци хэрхэн
нөлөөлөх вэ? Гэх мэт нь хоёр фазат загварчлалын гол асуулт болж байгаа юм. Мөн
үзэгдэлд ямар хүчин зүйлүүд нөлөөлдөг тухай, удаан хугацааны тооцооллын тухай
авч үзнэ.
Элсний тухай
мэдлэг.
Элсны орчны
үзэгдэл сайн судлагдсан сайтар мэдэгдэж байгаа, суух хурд нээх сүрхий асуудал
биш, гидродинамик үндэслэл, загварчлал баталгаатай тавигдсан, ёроолын харилцан
үйлчлэл мөн сайтар судлагдаж байгаа гэж мэт. Гэтэл шавар бол өөр хэрэг. Суух
хурд нь бөөгнөрөлөөс хамаарна. Энэ нь урсгалд нөлөөлнө. Элэгдэл нь критик
шүргэх хүчдэлээс хамаарна, суулт энэ тэр нь судлагдаж байгаа гэх мэт.
Загварыг урсгалын
хурд, гадаргын өндөржилт, ёроолын өндөржилтын өөрчлөлт зэргээр харьцуулж болно.
Хагшаасны концентраицйг хэмжиж харьцуулж болно. Турбулент шинж чанараар нь загвар
ба туршилтуудыг харцуулж болно.
Хагшаасны
бөөгнөрөлтийг агуулсан ба агуулаагүй нэг фазат урсгалууд байна. Хоёр фазат
бөөгнөрөлтгүй загвар мөн оршин байна. Бөөгнөрөлтийг тооцоолох маш олон томъёолол
байна. Шаврын бөөгнөрөлт нь хагшаасны зөөгдөлтийн загварчлалд нэгдүгээр
эрэмбийн нөлөөлөх хүчин зүйл болно. Хоёр фазат урсгалд бөөгнөрөлтийн туршилтын
томъёолол загварыг сайжруулах магадлалтай байна.
Санал болгож
байгаа 1 хэмжээст босоо хуваарилалтын хоёр фазат загварчлал нь бөөгнөрөлтийн
нөлөөллийг оруулж байгаагаараа ялгаатай юм байна. Загвараа хоёр голын ам дээр
туршсан байна. Томъёолол энэ тэрийг илтгэлд оруулаагүй байна. Суух хурд нь
5*10-4 м/с байна.
Хоёр газарт загвараар
тооцооллоо хийж бодит хэмжилттэй харьцуулжээ. Сайн ойролцоолсон байна.
Асуулт: Хагшаасны
суултанд тогтмол хурд хэрэглэсэн үү? Тооцсон гэнэ. Бөөгнөрөлтийн хэд хэдэн
нөлөөлөл суух хурданад нөлөөлсөн гэнэ.
Асуулт: хагшаасандаа
биологийн нөхцөл байдлыг авч үзсэн үү. Критик шүргэх хүчдэл болон элэгдэлтийн
коэфф нь биологийн хүчин зүйлээс хамаардаг.
Гүехэн усны хоёр
фазат урсгалын эгэл хэсгийн хүчдэлийн загварчлал дээр
Чаучат
Дууны концентраци
болон хурдны профайл нь ёроолын хагшаасны зөөгдөлтийг судлахад хэрэглэгдсэн
байна. Судалгаанд умбах тоо нь 1.1 ба шиелдсын дараметр нь 0.4 байна. Гурван
хэмжээст хоёр фазат урсгалын загвар ашигласан байна. 1985 оноос нимгэн урсгалын
үеийг судалж эхэлсэн ба ихэнх нь кинетик загварчлал дээр суурилдаг байна. Хатуу
хэсгийн даралтын нөлөөллийг мөргөлдөлт болон түр харилцан үйлчлэлийн нөлөөллөөр
тооцож шингэний даралт дээр нэмсэн байна. Харин хатуу хэсгийн харилцан үйлчлэлд
мөргөлдөөний болон үрэлтийн хүчдэлүүд нөлөөлж байна. Маш олон даралт болон
хүчдэлийн нөлөөллийг туршилт болон аналитик томъёоллоор оруулж өгсөн байна. К-эпсилон
загварт шинээр эсэргүүцэх хүчний сарнилтыг оруулж өгсөн байна.
Холигдох уртын
загварууд байна. СэдФОАМ (SedFOAM) гэдэг загвар open FOAM –ын санд түшиглэж боловсруулсан
байна.
3-р хэсэг.
Турбулент орчин, хатуу
маягийн зунгааралт.
Верзи
Туршилт хийсэн
байна. Хагшаас нь классик цилиндр хэлбэртэй. Туршилтаар мөргөлдөөний улмаас
хагшаас умбуур нөхцөлд ордог гэдгийг гаргаж ирсэн байна. Загварчлалд моментын
балансыг нэгтгэх тал дээр ажилласан байна. Кинетик онол дээр суурилж хагшаасны
шүргэх хчүдэлийг тодорхойлно. Моментыг нэгтгэсэнээр шингэний шүргэх хүчдэлийг
олно. Ингээд нөлөөлөх шингэний шүргэх хүчдэлийг олно. Зунгааралт нь гурван
хэсгээс бүрдэнэ гэж санал болгож байгаа юм байна. Зунгааралтын гидро динамик,
турбулент гидродинамик, хатуу маягын зунгааралт гэж байна гэнэ. Ингэж
илэрхийлсэн зунгааралт нь төлөвийн тэгшитгэлтэй холбоотой байна.
Асуулт: Шингэн ба
хатуу хэсгийн нягтын харьцаа хэд байсан бэ? Энэ миний туршилт биш. Гэхдээ
харьцаа нь 4.5 байсан.
Асуулт: Холигдох
замын уртын тухай.
ГЭГ аргаар нягтын
түрлэг/үйлчлэлийн тооцоолол.
Икари.
Үл шахагдах
нөхцөлтэй ГЭГ аргаар адвекци тархалтын тэгшитгэлийг шийдэж нягтын түрлэгийг
тооцно. ХЭХИ аргатай ижил олон төрлийн нэмэлт сайжруулалтыг ГЭГ аргад хэрэглэж
даралтын градиентад зөвтгөх матрицийг эргэлдэх моментод оруулж өгсөн байна.
Адвекц-тархалтын
тэгшитгэлээр тооцоолол хийсэн боловч хуримтлал, суултын нарийвчлал бага байсан
учир дахин эргэж харж засварлах хэрэг гарсан байна. Тунах хурдны загваруудыг
ашигласан боловч зарим нэг савалгаа байжээ. Загвараа бусадтай харьцуулсан ба ингэхдээ
түрэх ирмэгийн зайгаар нь мөн хэлбэрээр нь харьцуулсан байна. Тооцооны үр дүнд
одоогийн хэрэглэж байгаа даралтын градиент нь энэ төрлийн нягтын түрэлтийн
бодлогод тохиромжгүй гэдгийг тогтоожээ. Ирээдүйд хөрсний хэв гажилтад хэрэглэх,
орчны элэгдлийг тодорхойлох зэрэгт хэрэглэх болно.
Асуулт: Рейнольдсын
тоотой холбогдсон уу? Рейнольдсын тоотой холбогдоогүй. Түрэлтийн ирмэгийн хурд
нь Рейнольдсын тоотой холбоотой учир энэ талаас нь харвал сайн тайлбар гардаг
байна.
Асуулт: Хэвгийгүй
учир, туналт давамгайлна.
Том хуйлралтын
Эйлэрийн хоёр фазат загвар
Чен
Эйлер-Лагранжийн
аргачлал.
Эйлэр-Эйлэрийн
аргачлал.
Шүүсэн Эйлэрийн
хоёр фазат загвар гэдгийг боловсруулсан байна. Дэд торны загварыг хэрэглэсэн
байна. Шингэн ба эгэл хэсгийн дэд торны хүчдэл, дэд торны эсэргүүцлийн хүч гэх
мэтийг авч үзсэн байна. Хурдыг туршилт болон бусад загварчлалаар тооцсон үр
дүнтэй харьцуулбал зарим үед доогуур, зарим үед дээгүүр тооцоолсон байна.
Давхар тархалттай
хагшаажилт
Бурнс.
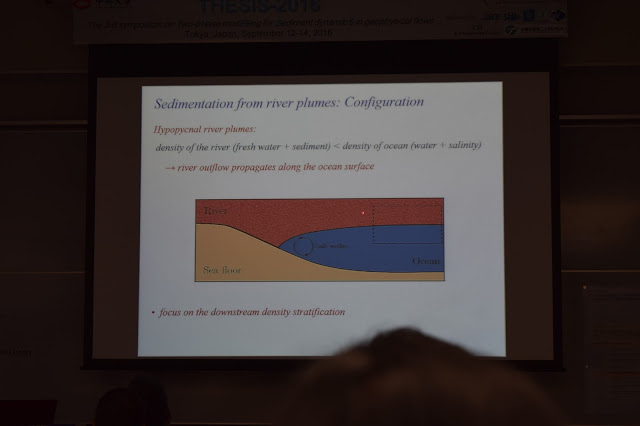
Далайруу цутгах
голын аман дахь асуудлыг үндсэн санаа болгосон байна. Далайн ус болон цэвэр ус
хагшаасны тухай авч үзэж байна. Хагшаастай ус давстай уснаас хөнгөн байх ба
тогтмол нөхцөлд байхаар тооцооллыг хийж үзье гэнэ. Парсон нар давстай устай
хагшаасыг цэвэр усны дээр байрлуулж давхар тархалтыг туршиж үзсэн байна.
Тархалт нь хуруулах эсвэл шүүрэх байдлаар тархдаг байна. Хагшаастай давстай ус
нь цэвэр ус болон давстай усны хооронд тогтворгүйжилт бий болгож үүнээс болж
шүүрэх эсвэл хуруулдах байдал үүсдэг байна. Смидтын тоо нь зунгааралтыг давсны
тархалтад харьцуулсантай тэнцүү байна. Хагшаас болон давсны тархалтыг харуулсан
байна. Хоёр ба гурван хэмжээстэд давхар тархалтын тооцооллыг хийсэн байна.
Давхар тархалт гэдэг нь ганц молекул тархалт биш мөн турбулент тархалтыг авч
үзсэнээр бий болно. Хамар гэсэн ойлголтыг гаргаж байна. Энэ нь нягтын зөрүүгээр
тайлбарлагдана.
Ширүүн урсгалтай үе дахь нягтын үйлчлэл, ёроолын хэлбэржилтийн туршилтын судалгаа.
Изүми
Хагшаажсан боомтуудын задралын үе дахь олон фазат урсгалыг загварчлах
Паик
Долгиолсон ёроол, умбуур хагшааснаас үүдэлтэй турбулент чанар
Ватанабэ
Хоёр дахь өдөр.
Урилгаар уншсан лекц - Олон хэмжээст олон
фазат хагшаасны зөөгдөлтийн загварчлалыг нээлттэй эх үүсвэр бүхий загварчлалын програмаар
гүйцэтгэх.
Хсү
Далайн эргийн
хувьсал нь далайн эргийн инженерчлэлийн гол судлагдахуун байдаг. Зарим
судалгааны хүндрэлүүдийн тухай илтгэнэ. Олон фазат загварчлалын тухай, түүний
баталгаажуулалтын тухай. Гурван шинжлэх ухааны тухай илтгэнэ.
Хэвтээ даралтын
градиент нь шүргэх хүчдэлээс илүүтэйгээр ёроолын хагшаастай холбогддог байна. Үүнийг
моментоос үүдэлтэй ёроолын эвдрэл гэнэ. Масштабны хуулиар мөлхөө үеийн зузааныг
тодорхойлоход нарийн ширхэгтэй элснүүдийн хувьд маш том гарч ирдэг. Умбуур
хагшаасны хэсгийн шингэрсэн зөөгдөлт гэж нэрлэдэг байна. Ёроолын хагшаас болон
умбуур хагшаасны хооронд үргэлж хагшаасны цүлхэлт байж байдаг. Турбулент урсгал
нь хагшаасны зөөгдөлтөнд маш чухал үүрэгтэй. Гурван хэмжээст төгсгөлөг эзлэхүүн
дээр суурилсан СэдФоам болон Пионеерс гэдэг хоёр хагшаасны нээлттэй эх
үүсвэрүүд байна. Эдгээр нь хоёр хэмжээст Эйлэрийн тэгшитгэл дээр үндэслэх нь
байна. Турбулент ойролцоололд Рейнольдсын дундаж НС, к-э загварыг хэрэглэж
болно. Харин гурван хэмжээстэд том хуйлралтын загварыг хэрэглэх нь байна. Энэ
тохиолдолд хагшаас мөн дахин шийдэгдэх боломжтой болно. Хоёр фазат урсгалд
кинетик энергийн балансыг хадгалах ёстой. Хөрсний реологийн загварыг ашиглан
мөлхөө үеийг загварчилж болох юм.
Яагаад нээлттэй
эх үүсвэрийг хөгжүүлж байгаа вэ гэхээр загварыг хүн бүр ирээдүйд ашиглаад
цаашаа явах боломжийг бүрдүүлж байгаад оршино. Гурван янзын хагшаасны
зөөгдөлтийн горим байна. Хамгийн эрчимтэй нь шингэрсэн зөөгдөлт, дараагых нь
хоёр үет зөөгдөлт, ламинаржсан зөөгдөлт гэж байна. Интермиттент үзэгдэл буюу
завсрын үзэгдэл нь тэдгээр зааг дээр бий болно. Буцах урсгал /урсгалын тодорхой
хэсэгт буцах чиглэлтэй урсгал үүсэх/ нь хагшаасны босолтонд мөн нөлөөлдөг
байна. РДНС турбулент ойролцооллоос Том хуйлралтын симуляцийг хагшаасны
босолтыг тодорхойлоход илүү нарийвчлалтай гэж үзэж байна. Хагшаасны ширхэглэл
нь Рейнольдсын тоо ихэсэх тусам хуйлралтыг багасгасан байна. CSDMS site
Асуулт: Нэг
инноваци нь к-э загвар дахь засвар гэж бодож байна.
Дугуйт элэгдлийн
Хоёр хэмжээст симуляцийг хоёр фазат урсгалаар шийдсэн нь.
Хөрсний элэгдэл
их чухал асуудал байх нь. Обьект дээр судалгааг боловсронгуй болгож урсгалыг
болон элэгдэлтийг хэмжиж хагшаасны зөөгдөлтийг үнэлсэн байна. Үүний дараагаад
дугуйт элэгдэлтийн туршилтыг хийж түүнийгээ хоёр фазат урсгалаар загварчилсан
байна. Эродиметер буюу элэгдлийн хэмжүүр хэмээх багаж байх ба түүгээр хөрсний
элэгдэлтийг судалдаг байна. Энэ нь зөөж байрлуулахад төвөгтэй учир дугуйн
хөдөлгөөнөөр элэгдлийг cудлах туршитыг хийсэн байна. Элэгдсэн хэсгээ лазер
профайлметерээр хэмжих ба дугуйны эргэх хурд болон дугуйн доод ёроолоос хөрс
хүртэлх зайнууд тэдгээрийн хамаарлыг судлах нь чухал байна. Хоёр фазат Эйлэрийн
загварыг боловсруулсан ба энэ нь гөлгөр биш учир ямар нэгэн итераци хийх
шаардлагатай байдаг банйа. Гурван хэмжээст WET загварыг хөгжүүлж байгаа юм
байна.
Асуулт: Хоёр
чухал параметр байна гэсэн. Өөр хүчин зүйл нөлөөлөх үү? Анхны хурдатгал
нөлөөлнө.
Турбулент урсгал
болон хагшаасны зөөгдөлтийн лабораторын туршилт.
Оцука
Элсэрхэг эрэг
дээр давалгаа цохиж өнгөрсөны дараагаар хагшаас босдог байна. 250 зураг 1 сек
авдаг өндөх хурдны камер байна. Хагшаасны босолт нь турбулент кинетик энергээс
бага хамаардаг байна.
Асуулт: Ач
холбогдолгүй асуулт асуугдсан.
Хайпар-концентарацитай
хагшаасны урсгал дахь нөлөөлөл.
Отомо
Хагшаасны концентрациас
хамааруулж урсгал дахь эсэргүүцлийн хүчийг тооцох ёстой юм байна. Энд
эсэргүүцлийн коэф-ыг туршилтын аргаар тодорхойлсон байна.
Гурван хэмжээст Бингхам
/гажиг шингэн/ шингэний урсгалын загварчлал
Кавасаки
Долпин гэдэг
програм
Хөрсны гулсалт
гэх мэт нь ньютоны бус шингэн учир Бингхамын шингэний шинж чанарыг үзүүлнэ. Хий
шингэн хатуу биеийн харилцан үйлчлэлийг тасралтгүй гадаргуугын хүчний загварыг
ашиглаж гадаргын таталцлыг нь загварчилдаг байна. Куб интерполяцийн түгэлт
гэдэг арга нь шингэний адвекцийг тооцоолох арга юм байна. Адвекцилахгүй алхамд
хялбарчилсан тодорхойлогч болон нүдний аргыг /marker and cell method/ хэрэглэнэ.
Хатуу биет нь маш өндөр зунгааралттай шингэнээр илэрхийлэглсэн байна.
Хагшаасны хэлбэр
түүний суух чанарт нөлөөлөх нь.
Ёокожима.
Хагшааслаг урсгал
чухал ойлголт. Энд хагшаасны хэлбэр маш их нөлоөөлнө. Умбуур хязгаарын нөхцөл
ашиглагдсан байна. Элсэн хагшаасны суултыг усанд туршсан байна. Хэлбэрээс гадна
орчин тойрны хагшаасны мөхлөгүүдээс суулт хамаарна.
Ганц болон олон
эгэл хэсгүүдийн урсгал.
Фукуока.
Ганц хагшаасны
мөхлөг хэрхэн тээвэрлэгдэхийг туршилт болон эйлэр-лагранжийн аргаар тооцсон
байна. Бөмбөрцөг хэлбэртэй хагшаас суугаад өнхөрч тээвэрлэгддэг бол бусад нь
ойх маягаар тээвэрлэгдэнэ. Бөмбөрцөгөөс бусад хэлбэртэй хагшааснууд нь бөөндөө
тээвэрлэгдэхэд харилцан үйлчлэл ба бөөгнөрсөн байдалтай зөөгддөг байна.
Хайргархаг
ёроолтой гол дахь хагшаасны хэлбэр, хэмжээний нөлөөлөх нөлөөлөл
Тодокоро
Олон хагшаасны
хэлбэрийг авч үзсэн байна. Хагшаасны хэлбэрийн
итгэлцүүрийг хүчний илэрхийлэлд оруулж өгч болох юм гэсэн санаа орж ирсэн.
Задарч буй умбуур
хагшаасны хоёр фазат загварчлал
Лее
Хатуу хэсгийн
хариу үйлдлийн хугацаа –
Хэлэлцүүлэг сургалт
Хагшаасны
зөөгдөлтийн динамик
Хуучин болон шинэ
тооцооны аргачлалуудын тухай
Өндөр
нарийвчлалтай олон хэмжээст хагшаасны зөөгдөлтийг загварчлах.
Шууд тооцооллын
симуляцийг авч үзэж хагшаасны динамикыг нарийвчлалтайгаар тооцсон тухай
хэлэлцэнэ. Хэмжээсээс хамаараад олон төрлийн тохиромжит загварчлал байгаа ба
тэдгээрийг нэгтгэн хялбарчилж бүх хэмжээстэд тохирсон загвар боловсруулах
хэрэгтэй. Тасралтгүй урсгал дахь шууд тооцооллын симуляци дахь нэг арга нь
шингэрсэн урсгалын загвар юм. Энэ нь 10-2-оос 10- хэмжээстэд тохирох
ба хагшаасны хэмжээс нь хагшаасны салалтаас хэд дахин бага байна. Инерцийн хүч
энэ тэр тооцогдохгүй орхигддог.
Шууд тооцооллын
ситмуляцын арга нь лабортаорын түвшинд тохирч байгаа ба хэрхэн том хэмжээстрүү
шилжүүлэх вэ гэдэг нь асуудал болж байгаа юм. Өндөр концентрацитай үед мөн
тохиромжгүй болж байгаа юм байна. Үүний дараагаар ширхэглэлийг дахин шийдвэрлэх
шууд тооцооллын симуляцийг боловруулсан байна. Энэ нь хагшаас хоорондын
харилцан үйлчлэлийг тодорхойлж чадна. Өөрөөр хэлбэл холбоослог хагшаасны
симуляцийг хийж чадна. Мөн л бага тооны хагшаасны эгэл хэсгийг авч үзэх учир
хязгаардагдмал байна. Өөр өөр загварчлалын группууд хамтарч ажиллавал ахисан үр
дүнд хүрэх байх гэж байна.
Хагшаасны
динамикийн механикыг эргэж хараад урагш төлөвлөх нь
Хагшаасны механик
туршилтаар эхэлж хагас туршилтруу шилжсэн. Энэ нь Мэеэр-Петер-Муллер нараар
эхэлж хар хайрцагний загварчлалаар үргэлжилсэн. Цүлхэлтийн арга нь хурд ба
концентрацийн үржвэрээр илэрхийлэгдэнэ. Дараа нь хагшаас хатуу хэсгээр
илэрхийлэгдэх болж хөдөлгөөний тэгшитгэл үйлчилж эхэлсэн. Эхэндээ цэвэр ус,
шингэний хурд өөрчлөгдөхгүй гэж үзээд Лагранжийн загварыг хэрэглэдэг байсан.
Хагшаас хоорондын
харилцан үйлчлэлийг салангид элементийн аргаар тооцох нь тохиромжтой болж
ирсэн. Ашида мичиуе хэмээх томъёоллыг гарган ирсэн байна.
Японы зчарим
тэргүүлэгч судлаачдын ажлууд, тэдгээрийн онцлогийг танилцуулав.
Эхнийх нь
салангид элемент, эйлэрийн хослосон арга.
Хоёр дахь нь олон
фазат урсгал турбуленттэй
Догшин урсгалтай
хэсэг
Практик чиглэсэн
арга – олон физикт симуляци – шингэн, байгууламж, хөрнсий харилцан үйлчлэлийн
тухай
Голын хагшаасны
зөөгдөлтийг тооцоолох шинэ аргачлал
Үчида
Хоёр фазат урсгал
гэж ву вэ? Гэдгийг тайлбарлана гэв.
Шингэний шууд
тооцооллын симуляци нь салангид элементийн аргатай холсож болно. Энэ нь
одоогийн байгаа хамгийн том хэмжээст тооцоолол байж магадгүй. Харин том
хуйлралтын загварчлалтай хослоход хэмжээс багасаж магадгүй. Хоёр хэмжээст
загварчлалын зураглалыг гаргасан байна.
Геофизикийн
түвшинд авч үзвэл бага хэмжээстэд хоёр фазат загварчлал оршин байгаа. Харин том
хэмжээстэд том хэмжээст гадны хүч болон хязгаарын нөхцлийг авч үзэх тооцоолол
байгаа боловч дунд хэмжээстэд хоосон орон зай буюу холбоос мэдлэг байхгүй
байна.
Уламжлалт тооцооллын
аргад хэд хэдэн дутагдал байгаа. Хагшаасны хэсэгт хагшаасны нийт эзлэхүүн нь
тэнцвэрт байх ба хагшаасны цүлхэлт нь зөвхөн босоо чиглэлд явагдана гэдэг нь
бодит нөхцөлд хэрэглэхэд дутагдалтай болж байгаа юм. Харин шингэний урсгалын
хувьд мөн дутагдал байна.
Уламжлалт
хагшаасны зөөгдөлтийн загварчлал
Хагас хэмжээст хоёр фазат загварчлал
Хагшаасны
загварчлалын суурь
Шинэ арга болон
хуучин аргачлал хоёрын хоорондох саад нь тэнцвэрт гэдэг нөхцөл байна. Энэ нь
ханын хууль болон хурданд байгаа.
Самбарын хэлэлцүүлэг
Уламжлалт аргад
-ёроолын хагшаас
- умбуур
хагшаасны томъёололууд
Шинэ аргачлалд
-
уламжлалт
аргад байхгүй зүйлс
-
хоёр
фазат загварчлалд хамааралгүй зүйлс
Хоёр фазат
загварчлал
-
хоёр
фазууд харилцан хамааралүйгээр хөдлөх боломжтой
-
хоёр
фазын харилцан үйлчлэлийг загварчилсан байх ёстой.
Ёроолын болон
умбуур хагшаасны томъёоллыг нэгтгэх боломж байгаа юу?
Эсвэл шингэний
чөлөөт гадаргуу болон давалгааны нөлөөллийг нарийвчлах ёстой юу?
Орон зайн
хэмжээсээс гадна хугацааны хэмжээ чухал байна.
Хүмүүс эхлээд бүх юмаа загварчилж
виртуал болгочихоод өөрсдөө араас нь орох байх.
Санал: бидэнд технологийн боломж байгаа учир
гидростатик бус даралтыг тооцоололд оруулах ёстой. Өөр нэг зүйл нь хатуу биеийн
механик/гранулар-мөхлөгийн физик байх ёстой.
Шинэ аргачлал нь
хоёр фазат урсгал бөгөөд энэ нь шингэн хатуу загвар, хатуу хатуу загваруудыг
агуулсан байна.
Ирээдүйн чиг
хандлага хагшаасны динамикт
Хоёр фазат урсгал
магадгүй хүчтэй загварчлал байх. Гэхдээ яагаад? Үгүй бол яагаад?
Хоёр фазат урсгал стандарт арга болох боловуу?
Англид практик ач холбогдол, академик ач холбогдлыг судалгааны төвүүд
үнэлдэг байх нь. Энэ тухай хийсэн бүх ажлууддаа хагас жилд нэг удаа тус бүр 2
хуудас ач хоблогдлын тухай тайлбар бичиг үйлддэг байна.
Гуравдах өдөр.
Уригдсан илтгэгч - Умбуур хязгаарын
нөхцөл түүний хөгжил болон хэрэглээг шингэрсэн ёроолд хэрэглэх нь
Луо
Туршилтын дулаан
дамжилт, шингэний механик, термодинамикийн олон улсын 6-р хурал-2014 он
Кажишима гэдэг
багштай уулзаж Умбуур хязгаарын нөхцлийг судалсан байна. Өмнөх профессороосоо
салангид элементийн аргыг сурсан байна.
Турбулент
урсгалын судалгааны төв – Станфорд их сургууль – д очиж сурсан байна.
Олон улсын хуралд
байнга оролцож байх нь хамгийн чухал бөгөөд үргэлж залуу сэтгэлгээтэй байх
хэрэгтэй гэдгийг шинэ залуу судлаачидад захиж хэлэв.
Умбуур хязгаарын
нөхцөл
15 жилийн
түүхтэй. 1972 онд Дескин гэдэг хүн хүний зурхний цусны урсгалыг судлахад анх
ашигласан байна. Хамгийн чухал нь хэд хэдэн нэмэлт гишүүд ордог байна.
Интерполяци, зөвтгөл гэх мэт нь байнга хийгдэж хязгаарын тооцоолж байдаг. Гурван
чухал бүсийг авч үзэх ба эхнийх нь шингэн, хязгаар, хатуу бүсүүд байна.
5 төрлийн умбуур
хязгаарын нөхцлийг хувилбарууд хэрэглэгдэж байна. Анхны умбуур хязгаарын нөхцөл
нь эластик загвар хэрэглэж хүчийг тооцдог байж.
Шингэн хатуу
хэсгийн харилцан үйлчлэлийг тооцох шууд хүчний арга нь 16 жилийн өмнө танилцуулагдсан
ба хурдыг дундажилж түүгээрээ хүчээ тооцдог байна. Шууд хүчний арга нь хэд
хэдэн хувилбар байх ба эйлэрийн торон дээр умбуур биеийн лагранжийн цэгүүдээр
дамжуулж хурдаар тодорхойлох ба хатуу биеээр нийлбэрчлэл авч үндсэн хүчийг
олно.
Хүчийг тооцох өөр
нэг арга нь хоосон хиймэл арга, умбуур харилцан үйлчлэлийн арга гэж байна.
Хурдыг цуваанд задалж тоцоолно.
Нүдийг тасдах
аргуудаас
Өөр өөр умбуур
хязгаарын нөхцлүүд олон давуу болон дутагдалтай талуудтай. Хэрэглээ нь арвин
байна.
Яаж тооцооллын
нарийчлалыг сайжруулах вэ? Түүнийг сайжруулах
Эхлээд шугаман
бус интерполяцийн стратеги
Хязгаар дээрх
хурдыг олохдоо шугаман бус аргыг хэрэглэх ба шингэн ба хатуу хэсгийн харилцан
үйлчлэлд үр ашиг нэмэгдэнэ. Нэг хүч хэрэглэсэнээс хугацааны алхамд олон хүч
хэрэглэсэнээр үл гулсах нөхцөл бүрэн сайжирна.
Умбуур хязгаарын
нөхцлөөр дулаан дамжилтыг мөн тооцсон байна.
Хувирамтгай/дасан
зохицох хэлхээсийг хэрэглэсэн байна. Мөн шаталтанд хэрэглэж эхэлсэн байна. Цэгэн
эгэл хэсэгт умбуур хязгаарын аргыг хэрэглэж болох нь.
Шингэрсэн ёроолд
хэрэглэх нь.
Умбуур хязгаарын
нөхцлийг шууд тооцооллын симуляцид нэгтгэхдээ хэдэн нэмэлт хийдэг байна. Хийсэн
тооцоонуудых нь хугацааны алхам 10-6 зэрэгтэй байна. 28800 СПҮ
хугацаанд 1 физик цагын үр дүнг гаргаж авч байна гэнэ.
Хурдтай тунаж
байгаа хатуу хэсгүүдийн эргэн тойронд агаарын бөмбөлөг үүсдэг байна. Үүнийг
тооцож чаддаг.
Эсэргүүцлийн хүч
дээрх зарим нэг асудал байгаа бололтой.
12 торонд 1 эгэл хэсэг таарахаар геометр ойролцооллоо
хийсэн байна. Шингэний тэгшитгэлүүдийг хүчний цувааны аргыг ашиглан ойролцоолж
боддог байна. Ялгаварын аргыг хэрэглэдэггүй.
Микро сүвэрхэг
орчинд доторх эгэл хэсгийн зөөгдөлт
Ишигами
Зарим сүвэрхэг
орчинууд нь фазын ялгаралтаар бий болдог байна. Фазын орны загвар
Вандерваалсын
тэгшитгэл нь харилцан үйлчлэлийн хүчний тухай тэгшитгэл ба тодорхой орон зай
байжийж эгэл хэсэг хана хоорондын харилцан үйлчлэлийг судлах, тооцох юм байна.
Рейлагийн тоон
дээр суурилсан шингэн хату хэсгийн харилцан үйлчлэл дахь дулаан дамжилтын
нөлөөлөл
Гү, Такеучи,
кажишима
Мөн умбуур
хязгаарын нөхцлийг хэрэглэсэн байна. Үндсэн хугацааны дэвшилд жижигхэн хурдны
өөрчлөлт хийсэн байна.
Гурван фазад
урсгалын тооцоолол
Сан болон Сакай
Уул уурхайн
булинга нь энэ урсгалын гол жишээ юм. Салангид элемент-Шингэний эзлэхүүний арга.
Орчны эзлэхүүний дундажлах аргаар харилцан үйлчлэлийг тооцоолсон байна. ШЭА
ашиглагдаж байгаа учир хатуу эгэл хэсэг альч фазад нарийн тодорхойлогдоно.
Дурын хэлбэртэй
хязгаарын арга Шгето-Сакай 2014
Маттуттис
Салангид
элементийн арга ба төгсгөлөг элементийн арга
Энэ удаад
болохгүй байгаа зүйлсийг танилцуулна. Шаталсан хязгаар ашиглахад хязгаарын урт
үргэлж адил байна. Velocity plotted over time
Simulation lost –
try – no effect
Төгсгөлөг
элементийн арга дахь шугаман аргачлал нь шугаман бус НС тэгшитгэлийг хөдлөх
хязгаарын нөхцөлтэйгээр тооцоолж чадахгүй байна гэдэг нь тулгараад байгаа
асуудал юм.
Заримдаг 3
хэмжээст хоёр фазат загварчлалыг шингэн ба хагшаасанд хэрэглэх.
Үчида
Ёроолын хурдны
тооцооллын арга гэдгийг танилцуулж хоёр хэмжээстэд оруулж өгсөнөөр заримдаг
гурван хэмжээсийн арга гарч ирнэ. Санаа нь хуйлралтын тэгшитгэлээс гарч ирсэн
байна. Динамик хананы хуульд хуйлралтын үе, барзгаршилтын үе гэсэн чухал
ойлголтууд гарч ирнэ.
Турбулент урсгалд
гүнээр дундажилсан турбулент энергийг дэд гүний хэмжээст турбулент хэмээх
аргаар боджээ.
Гурван хэмжээст
орчны элэгдлийг гибрид Эйлэрийн аргаар тооцоолох
Ота, Сато нар
Эйлэр-Лагранжийн
арга
Турбулентийг шууд
тооцооллын симуляци аргаар бодсон байна. Хагшаас босох, суух процессуудыг
анхаарч үзсэн байна. Хагшаас босох болон суух эзлэхүүнүүдийг статистик аргаар
тодорхойлж томъёолсон байна.
Давалгаа
таслагчийн орчим дахь элэгдлийг хоёр фазат загварчилалаар тоцоолох
Бактиари
ГЭГ болон СЭА
зэргийг хослуулж тооцооллыг хийсэн байна.
Далайн ёроолын
хариу үйлдлийг ЛБА-аар судлах
Lee Xie
Wave boundary layer over stone-covered bed 2008 – өгүүллийг олж унших хэрэгтэй юм
байна.
Сүүлчийн хэсэг
Цунамигаас
үүдэлтэй орчны элэгдлийн загварчлал
Накамура, мизутани
Ус хөрс барилга
хагшаасны загварчлал – Шингэний эзлэхүүний арга, хагшаасны зөөгдөлтийн
загварчлал
Энгэлүнд ба
Фредсо нарын ёроолын хагшаасны загварчлалыг хэргэлэсэн байна. Критик шиэлдсийн
параметр ёроолын хагшаасны зөөгдөлтөнд чухал ач холбогдолтой. 1/100 харьцаатай
физик загварчлалыг үйлдэж түүнийгээ тооцооллын аргатай харьцуулсан байна.
Цунамигийн
түрлэгээр бий болох элэгдэл ба барилгын тогтворшилтын тухай
Назеса
Хоёр фазат сулхан
үл шахагдах ГЭГ арга
Ахмед - Хоккайдо их сургууль
ГЭГ-ийн нөлөөллийн хүрээнд хоёр фаз бүхий эгэл
хэсгүүд оршино.
Шүүрэлтээс
хамааралтай далангийн нуралтууд
Онда
Төгсгөлөг
элементийн хязгаарт тааруулсан торыг ашигласан байна. Эластик-дласто
ойролцоолол.
Дугуй ширээний ярилцлага буюу хаалт
Инженерчлэлд юу
хэрэгтэй вэ гэдгийг авч үзэх ёстой. Ихэнх аргууд барилгын инженерчлэлд анх бий
болоогүй. Тооцооны аргачлалын хөгжлийг бид өнгөлөөгүй араас нь дагаад явж
байна. Бид усны инженерүүд, бидэнд хамаатай асуудлуудыг өөрсдөө оройлон шийдэх
хэрэгэй байна гэсэн санаа хүн бүрээс гарч байв.
Дараагийн хуралд
хэлэлцүүлгийн оронд тодорхой нэг сэдвээр семинар хийвэл ямар вэ? Өөр өөр
салбарын хүмүүсийг илүүтэй оруулах нь салбар бүр тийш мэдлэг тэлэх болно. Хоёр
фазат урсгалын жишиг бодлоготой болох хэрэгтэй гэсэн санал гарав. Мөн жишиг
мэдээлэлтэй болох. Жишиг бодлого нь амархан бөгөөд төвөгтэй физик үзэгдлийг
агуулсан бах ёстой.
Жишиг бодлого нь
байгаль дээрх хэмжилийн мэдээнээс бүрдэх ёстой болов уу? гэж зарим эрдэмтэд
хэлэв.
Хуралд тавигдсан ханын илтгэлүүд
No comments:
Post a Comment