Тооцонгийн үр дүнд суурилж морь унах нь (The riding horse based on scientific computation)

Шингэний динамикийн тооцоонд үндэслэж морь унавал...

Магистраа төгссөнөөс хойш мөрөөдөж байсан, маш удсан, оролдлого хийж чададгүй байсан нэг мөрөөдөл, хүсэл бол өндөр бүтээмжтэй тооцоололыг (high performance computing) супер компьютер эсвэл параллель тооцоолол хийх боломжтой багцан (super computer or GPGPU cluster) дээр хийх явдал байсан юм. Тооцон бодох тооцооны аргуудыг мэдэхгүй, код бичиж чадахгүй, ямар ч програмчлалын хэл эзэмшээгүй байж юун өндөр бүтээмжит тооцоолол хийх гэдэг нь ойлгомжтой. Тэгээд ч суурин компьютер, эсвэл зөөврийн компьютерээс өөр зүйл бидэнд /Монголд/ олдох биш. Интернэтээр ингэж супер компьютер ашиглаж ийм тооцоолол үйлдэж ийм үр дүн гаргалаа гэх мэт өгүүлэл, бичлэгийг харж гайхан бишэрч мөрөөдлөө бүр л биелүүлмээр санагддаг байж билээ. Докторт сурахаар /2014 оны 9 сар/ Нагаокагийн Технологийн их сургуульд ирэхдээ тооцон бодох хэдэн арга эзэмших, код бичиж сурах, бүх боломжит бодлогонуудыг бодож чаддаг болох гэх мэт л үндсэн чухал зорилтууд өвөртлөж байсан юм. Тэгтэл бараг жилийн дараа /2015 оны 6 сар/ сургуулийн зарын самбар дээрээс GPGPU сургалтын тухай Япон зар байхыг олж харсан юм. Ингэхэд л энэ сургуульд GPGPU байдаг юм байна гэж мэдэж билээ. Тэгээд ч энэ сургалтын боломжийг ашиглаж чадаагүй, хийх ажил ихтэй байсан учир сонирхолгүй орхисон. Гэхдээ л ашиглаж үзэх хүсэл байгаад л байлаа. Ядаж барааг нь нэг удаа харах юмсан гэж бодож байсан юм. 

Үүний дараа 2016 оны 1 сард ЛБА-аар GPGPU дээр хэрхэн тооцоолол хийх тухай семинар болно гэдгийг удирдагч багш маань дуулгаж за энэ боломжийг л ашиглаж GPU тэй танилцая гээд танилцсан юм. Хэрхэн танилцсан тухайгаа нийтлэл болгож бичсэн байгааг зарим нэг нь болгоосон байхаа. Нийтлэлийг эндээс

Хэдий танилцаад авсан ч шууд GPU -рүү орох боломж байгаагүй тул хэрэгтэй гэсэн болгоноо нийтлэл дээрээ бичээд 2016 оны 7 эсвэл 8 сараас нэг ашиглаж үзнэ гээд төлөвлөгөөндөө орууллаа. Төлөвлөгөө жаахан сунжирч одоо /2016 оны 10 сар/ л нэг оролдож байна даа. 

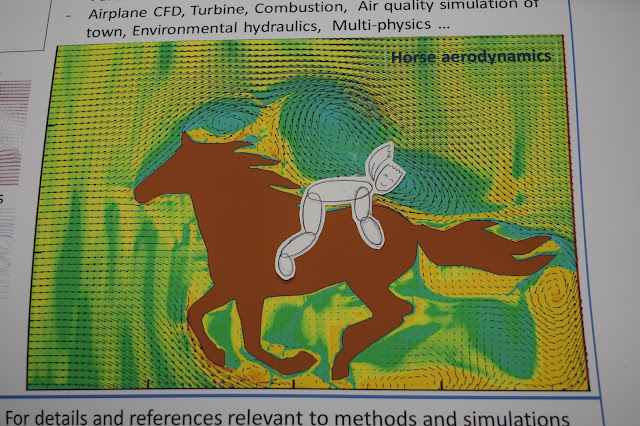
Өөр нэг мөрөөдөл болох Монгол уламжлалтай холбоотой зүйлсийн шингэний динамикийн тооцоог хийж судалж үзэх юмсан гэсэн хүсэл бас л их удаж байна. Үүний нэг нь Монгол морины аэродинамикийн тооцоолол юм. Хүлэг морь бол Монгол түмний шүтээн, хамгийн хурдан унаа учир морио л тооцож үзмээр санагдаад тэгээд тооцсон хэрэг. Энэ нийтлэлд энэ тухай авч үзнэ. 

Давхиж буй морины аэродинамикийн загвар Рэйнольдсын тоо 3000.

Морь зурж өссөн болхоор морио зураад компьютертээ хийгээд параллелиар кодлоод загварчилсан хэрэг. Координатын эхийг бодлогын хүрээний буланд сонгоод морины хэлбэрийг харуулах гадаргуугын зураасны координатуудыг тоон цуваа болгож авбал (Лагранжийн цэгүүд):

108.083916 386.28964
107.41259 378.74893
106.74126 373.26477
106.74126 366.4096
106.06993 363.6675
102.04196 360.23993
99.35664   356.81235
98.013985 350.64267
93.31468  347.9006
87.27273  343.10196
83.24476  338.30334
77.2028    332.81918
69.818184 325.2785
60.41958  317.05228
53.706295 310.19708
45.65035  301.97086
41.62238  297.17224
40.95105  288.946
42.965034 280.03427
46.993008 275.23566
55.04895  273.17908
61.762238 275.92117
68.475525 281.4053
73.84615  284.83292
83.24476  288.2605
89.28671  288.946
100.02797 288.946
108.75524 290.31705
116.81119 290.31705
124.1958  286.88947
128.89511 273.86462
132.25175 257.41217
137.62238 243.01628
Энэ тоон өгөгдлөөр зурагдах морь нь доорхи шиг харагдана. Энийг тооцоонд оруулж хязгаарын нөхцлийг өгч бодуулна. 

Толгойг нь зөв харуулсан учир буруу тийш харсан байгаа шүү.

Энэ мэдээгээ загвартаа дуудаж оруулах код нь: 

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19

!--- ! input for flag !--- subroutine readaflag(index) use SimulationParameter implicit none integer :: i,j integer,intent(inout) :: index(1:Nx,1:Ny) index=1 ! read flag from file open(unit=921,file="grid.dat",action="read") do j=1,400 read(unit=921,*) (index(i,j), i=50,770) end do close (921) end subroutine readaflag

ЛБА нь дурын хэлбэр бүхий геометр дүрстэй бодлогыг бодоход маш тохиромжтой учир морины хэцүү хэлбэр бол нээх асуудал биш юм. Бодлогод хоёр хүлцэл авч байгаа юм. Эхнийх нь морь хөдлөхгүй, өөрөөр хэлбэл морины хөдөлгөөнийг бодлогод оруулаагүй, дээрх шиг нэг зураг л бодлогод хэрэглэгдэнэ гэсэн үг. Хоёр дахь нь хоёр хэмжээст тооцоолол юм. Одоохондоо 3 хэмжээст код бичээгүй байгаа учир тэр л дээ. Морины давхих хөдөлгөөний нэг циклийг долийн нарийвчлалтай мэдээлэл байдлаар гаргаад авбал давхиж яваа морийг загварчилж болох л байх. Үүнийг ирээдүйн тооцон бодогч инженерүүд, эсвэл өөрөө хийх байхаа. 

Энгийн ЛБА-аар том хэмжээстэй иймэрхүү бодлогыг бодоход хугацаа их зарцуулна. Дээрээс нь өндөр Рейнольдсын тоотой учир бараг л чадахгүй болов уу. Тиймээс Энтропик ЛБА-ыг хэрэглэж байгаа юм. Үнэндээ Энтропик ЛБА-ын физик утгыг мэдэхгүй байгаа ч Хэнмэдэх багшийн ачаар кодлоод авчихсан байгаа. Энэ талаар бид судалгааны ажил хийж ханын илтгэл тавьж сэтгүүлд өгүүлэл өгсөн байгаа. 

Энд зөвхөн түгэлтийн функцуудын бүрдүүлэгчүүд, тогтворжуулагчийг хэрхэн тооцох цуваа кодыг оруулж тайлбарлана. Түгэлтийн функц хэмээх гол хэмжигдэхүүн ЛБА бий. Энэ түгэлтийн функцыг задалж үзвэл кинематик, шүргэх хүчдэлтэй хамаатай хэсэг болон өндөр эрэмбийн хэсэг гэсэн бүрдүүлэгчүүд байна. Эдгээрээр нь ЛБА-ын нэг алхам болох мөргөлдөх алхамыг гүйцэтгэх боломж байгаа ба мөргөлдөх алхамд Энтопи функцын хамгийг бага байх нөхцөлд олдож буй тогторшуулагч параметрийг ашиглана. Мөргөлдөөний оператор:

Энд байгаа шүргэх хэсгийг

харин өндөр эрэмбийн хэсгийг

гэж олох ба тогтворшуулагчийг

гэж олохнээ. Эдгээрийг Фортран 95 хэлээр кодловол:

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84

!--- ! Entropic: calculating population parts, shear and higher order one !--- subroutine populationParts(f,f_eq,velx,vely,dens,d_s,d_h,gamma) use SimulationParameter implicit none real(8),intent(in) :: f (First:Last,1:Nx,1:Ny) real(8),intent(in) :: f_eq(First:Last,1:Nx,1:Ny) real(8),intent(in) :: velx(1:Nx,1:Ny) real(8),intent(in) :: vely(1:Nx,1:Ny) real(8),intent(in) :: dens(1:Nx,1:Ny) !entropic variables real(8),intent(inout) :: gamma(1:Nx,1:Ny) real(8),intent(inout) :: d_s(First:Last,1:Nx,1:Ny) real(8),intent(inout) :: d_h(First:Last,1:Nx,1:Ny) !entropic local variables real(8) :: m11,m02,m20 !natural moments real(8) :: summ11,summ02,summ20,sum02,sum20 real(8) :: Pxy,Nxy,uxy2,uxy,N_x,N_y,N22,Txy,Tx,Ty integer :: i,j,k gamma(:,:)=1d0/CoefRelax ! calculation of natural moments do i=1,Nx do j=1,Ny summ11=0d0 summ02=0d0 summ20=0d0 do k=First,Last summ11=summ11+f(k,i,j)*ConvVelx(k)*ConvVely(k) summ02=summ02+f(k,i,j)*ConvVely(k)**2 summ20=summ20+f(k,i,j)*ConvVelx(k)**2 enddo m11=summ11/dens(i,j) m02=summ02/dens(i,j) m20=summ20/dens(i,j) Pxy=m11-velx(i,j)*vely(i,j) Nxy=m20-m02& -(velx(i,j)**2-vely(i,j)**2) uxy2=(velx(i,j)**2-vely(i,j)**2) uxy =velx(i,j)*vely(i,j) N_x=velx(i,j)*Nxy N_y=vely(i,j)*Nxy N22=uxy2*Nxy Txy=uxy*Pxy Tx = velx(i,j)*Pxy Ty = vely(i,j)*Pxy d_s(0,i,j)=dens(i,j)*(4d0*Txy - N22/2d0) d_s(1,i,j)=0.5d0*dens(i,j)& *(((Nxy+N_x+N22)/2d0)-(2d0*Ty+4d0*Txy)) d_s(2,i,j)=0.5d0*dens(i,j)& *(((-Nxy-N_y+N22)/2d0)-(2d0*Tx+4d0*Txy)) d_s(3,i,j)=0.5d0*dens(i,j)& *(((Nxy-N_x+N22)/2d0)-(-2d0*Ty+4d0*Txy)) d_s(4,i,j)=0.5d0*dens(i,j)& *(((-Nxy+N_y+N22)/2d0)-(-2d0*Tx+4d0*Txy)) d_s(5,i,j)=0.25d0*dens(i,j)& *((4d0*Txy+Pxy+2d0*Tx+2d0*Ty)+((-N_x+N_y-N22)/2d0)) d_s(6,i,j)=0.25d0*dens(i,j)& *((4d0*Txy-Pxy+2d0*Tx-2d0*Ty)+((N_x+N_y-N22)/2d0)) d_s(7,i,j)=0.25d0*dens(i,j)& *((4d0*Txy+Pxy-2d0*Tx-2d0*Ty)+((N_x-N_y-N22)/2d0)) d_s(8,i,j)=0.25d0*dens(i,j)& *((4d0*Txy-Pxy-2d0*Tx+2d0*Ty)+((-N_x-N_y-N22)/2d0)) sum02=0d0 sum20=0d0 do k=First,Last d_h(k,i,j)=f(k,i,j)-f_eq(k,i,j)-d_s(k,i,j) sum02=sum02+d_s(k,i,j)*d_h(k,i,j)/f_eq(k,i,j) sum20=sum20+d_h(k,i,j)**2/f_eq(k,i,j) enddo gamma(i,j)=1d0/CoefRelax-(2d0-1d0/CoefRelax)& *sum02/(sum20+10d-8) enddo enddo ! calculating stabilizer end subroutine

Хүлэг морины тооцоог 800*800-ийн том торон дээр үйлдсэн юм. 
Зарим хүмүүс яаж GPGPU-тэйгээ холбогдож тооцоо хийдэг вэ гэж бодож магадгүй. Тооцоо хийх гэж байгаа машинтайгаа winscp гэдэг протоколоор холбогдож файлуудаа авч хийж зохицуулна. 

Өөрийн компьютераасаа файлаа шууд GPGPU -ийн сэрвэрлүү хуулаад гарсан тооцооны үр дүнгээ бас шууд хуулаад авах боломжийг энэ програм бүрдүүлнэ. Харин тооцоо хийхдээ tera term гэдэг консоль дээр Линуксийн үйлдлээр харилцана. 

Улаан дөрвөлжингөөр яаж КУДА Фортран кодыг хөрвүүлэх аргыг харуулсан байгаа. Хамгийн доод хэсгийн мөр бол хөрвүүлэгдсэн файлыг машинаар бодуулах комманд юм.
Морины орчин дахь урсгалын үр дүнг гаргаад авчихлаа. Одоо яах вэ? Юунд хэрэгтэй вэ гэхээр морины давхих хурданд унаач хэрхэн нөлөөлдөгийг, унах хэлбэр хэр нөлөөлөхийг тооцож үзэж болно.

Энэ бол давхиж буй морины орчимд үүсэж буй агаарын ургалын хуйлралтыг харуулж байна. 

Үндсэндээ морины дэл орчимд нуруу дагасан хуйлралт морины толгойноос эхэлж гарч ирдэг байна. Морь давхихдаа ихэвчлэн хүзүү нь эгцэрч урагш чиглэдэг нь бага гидродинамик ачаалал ирдэгтэй холбоотой байж болох юм. Хурдны морь толгойгоо өргөөд дээрх морь шиг давхидаггүй нь аль болох өөрийн хурдаар үүсгэх агаарын ургалын бага эсэргүүцлийг бий болгож дасан зохицож давхидаг юм шиг. Морины согсоо, сүүлийг боодог нь үс сарвалзаж саад болохоос сэргийлэхээс гадна урсгалын эсэргүүцлийг багасгадаг байж болох юм. Энэ талаар дэлгэрүүлж судлах боломж бий. Ер нь моринд далавч өмсгөөд өгчихвөл зээр шиг дүүлж магадгүй шүү.....

Үүнээс гадна морь унаач нь морины цуцах, хурдлах эсэхэд маш их нөлөө үзүүлнэ. Энэ морийг унаачгүй тооцсон нь учиртай бөлгөө. Учир нь гэвээс: 

Ханын сонинд сонирхолтой хэсэг нэмсэн юм. Унаачгүй морь, унаач нь зочин.

Морь ямар байдлаар мордож давхивал моринд бага эсэргүүцэл үзүүлэх вэ гэдгийг ГИГАКҮ олон улсын хуралд тавьсан ханын илтгэлийн үеэр үзэгч зочидоос асууж жаахан хөгжилдсөн юм. Дөрвөн төрлийн морь унах хэлбэрийг зураад үзэгчдээс өөрөөр нь сонгуулсан юм. Морины уралдаан үзэж байсан бол төвөггүй л сонгоно. Ер нь хийж байгаа ажлаа аль болох чанарын өндөр түвшинд гүйцэтгэх нь ажлын зарчим байх ёстой. Тйимээс тавьж буй ханын илтгэл болгоноо сонирхолтой байлгах гэж хичээсний нэг жишээ энэ юм. Хүмүүс зөв хэлбэрийг сонгож байсан нь илтгэлээс юм ойлгосоны баримт юм гэж ойлгоно. 
Ингээд хэлбэрүүдийг авч үзье ээ. Эдгээрт хөгжилтэй нэрсүүдийг өгсөн юм. 

Мэргэжлийн унаач (professional rider)

Энгийн унаач (common rider)

Согтуу унаач эсвэл орнгироо унаач (Drunken rider)

Дэггүй унаач (mischievous rider)

Аль хэлбэр нь моринд болоод таньд таатай гэж бодож байна ? 
1 - бол хурдын морийг ингэж унавал өөрт болоод моринд таатай байна. Агаарын эсэргүүцэл бага, салхинд бага цохигдоно. 
2 - бол моринд эсэргүүцэл ихтэй, өөрт амар эгцээрээ суусан учир. Энэ хэлбэрээр хэсэг зуур л давхихад тохиромжтой. Эмээл дээрээ босвол бүр л их эсэргүүцэл үзүүлнэ. 
3 - Согтуу нөхдүүд маль тамлаж байгаагаа мэдэх биш. ккк. Эсэргүүцлийн хувьд 2-оос арай бага байж магадгүй. Гэхдээ морь унаачын биеийн байрлалыг мэдэрч давхидаг учир оновчгүй л байрлал. 
4 - Циркчид. Бага байхад зарим нь ингэж унадаг л байсан юм. Энэ бол гидродинамикийн хувьд маш тохирмжой боловч унаачдаа тохиромжгүй, жолоодоход хэцүү байрлал байна. 

Энэ мэтээр шинжлэх ухаанч байдлаар юмсыг судалж уламжлалын хүрээнд засаж сайжруулах зүйлсийг сайжруулах хэрэгтэй.