Гүехэн усны тэгшитгэлийн гаргалгаа
 |
| Номхон далайн талд байрлах Японы Камакура хэсэгт бий болох боломжит Цунамигийн загвар: Гүехэн усны тэгшитгэлээр тооцон бодсон жишээ. Credit to Prof. Hosoyamada Tokuzo. Source: paper |
Гүехэн усны тэгшитгэл нь инженерийн гидравликийн, тэр дундаа тооцон бодох гидравликийн хувьд маш чухал тэгшитгэлүүдийн нэг юм. Энэ тэгшитгэлийг гаргаадаггүй болчиховол янз бүрийн үерийн усны, гол мөрний, далай тэнгисийн загварчлалыг хийх боломжтой болно. Дан ганц гидравлик, далайн урсгал гэлгүй, агаарын урсгалыг загварчилахад мөн ашиглагдана. Ингээд энэ тэгшитгэлийн гаргалгааг авч үзье ээ.
 |
| Вики дээрх гүехэн усны тэгшитгэлээр бодсон усны долгионы дүр зураг |
Гүехэн усны тэгшитгэл нь шингэний
хөдөлгөөний хэвтээ урсгалыг хүндийн хүчний нөлөөнд дүрслэн харуулах Навьер-Стокесийн
тэгшитгэлийн хялбаршуулсан хэлбэр юм. Гүехэн усны тэгшитгэлийг мөн
Сайнт-Винантын тэгшитгэл гэж нэрлэдэг. Ингээд гүехэн усны тэгшитгэлийн
гаргалгааг үндсэн тэгшитгэлүүдээс гаргая. Үүний тулд эхлээд үл агших шингэний
урсгал тасралтгүйн тэгшитгэлийг авч үзвэл
байх ба үүнийг босоо чиглэлийн
дагуу гадаргуугын ирмэгээс усны чөлөөт гадаргуу (ямар нэгэн хоёр ялгаатай урсгалын зааг) хүртэл нийлбэрчилбэл
Лейбницийн интегралын дүрмийг
хэрэглэвэл хоёр хэвтээ хурдны диффенциалууд:
Илэрхийлэл 2-ыг 1-д оруулж бичвэл
болно. Шингэний ёроол буюу газрын
гадаргуу дээрх хананы нөхцөл, шингэний чөлөөт гадаргуу дээрх кинематик
нөхцлүүдийг босс хурданд авч үзэх шаардлагатай ба тэдгээр нь:
Нөхцөл 5-ыг тэгшитгэл 4-д
орлуулбал
болж гүехэн усны урсгал
тасралтгүйн тэгшитгэл гарч ирнэ. Энэ нь чөлөөт гадаргуугын өөрчлөлт нь хэвтээ
чиглэлийн нэгж зарцуулгуудын өөрчлөлттэй эсрэг байна гэдгийг харуулж байна.
Одоо Навьер-Стокесийн
тэгшитгэлээс гүехэн усны хөдөлгөөний тэгшитгэлийг гаргая. Үүний тулд босоо
тэнхлэгийн дагуур Навьер-Стокесийн тэгшитгэлийн бүрдүүлэгчийг бичвэл:
байх ба гүехэн усанд босоо
чиглэлтэй хурдны градиент тооцогдохооргүй бага байна гэсэн нөхцлийг авч үзвэл
дээрх тэгшитгэл хялбарчилагдан
болно. Энийг ёроолоос чөлөөт
гадаргуу хүртэл интералчилбал гидростатикийн тэгшитгэл
гарч ирнэ. Тэгшитгэл 9 – ийг
НС-ын тэгшитгэлийн бусад хоёр бүрдүүлэгч болох х ба у чиглэл дахь
тэгшитгэлүүдэд даралтын оронд орлуулбал
Тухайлбал тэгшитгэл 10-ын зүүн
талын илэрхийллийг урсгал тасралтгүйн тэгшитгэлээр баяжуулбал:
(үржвэрийн дифференциал дүрэм
хэрэглэгдсэн) болох ба үр дүнд нь хөдөлгөөний тэгшитгэл
у чиглэл үүнтэй яг ижилхэн байна
гэдгийг санаарай. Одоо тэгшитгэлийн зарим илэрхийллийн дифференциалыг
интегралаар солихын тулд Лейбницийн дүрмийг ашиглана. Тэгшитгэл 11 дараах
байдалтай болно:
Дээрхээс тус бүрд нь задалж
бичвэл:
Эдгээрт s, b гэсэн дэд индексүүд нь гадаргуу болон ёроол гэсэн
утгатай ба хурднууд нь гадаргуу ба ёроолд байгаа гэдгийг илтгэнэ. Дээрхийн
интегралтай хэсгийг нь орхиод хэвтээ ба босоо хурдтай хэсгүүдийг нь бүлэглэж
ялгавал
Гаргалгаа 12f –ийн гадаргуугын буюу ёроолын хувьсалыг үл тооцно
гэсэн нөхцлөөр тэг болж байгаа юм. Дээрхүүдийг нэгтгэвэл тэгшитгэл 12-ын зүүн
талын интеграл
болж хялбарчилагдана. Харин
баруун талын гишүүдийг
гэж хялбарчилж болох ба тэгшитгэл
13 ба 14-ийг нэгтгэж etta+h -д хуваавал:
болно. Үүнд дараах хялбаричлгаанууд
ашиглагдсан:
үүнд u нь гүнээр дундажилсан хурд, betta нь моментын засварын коэффициент зэрэг болно.















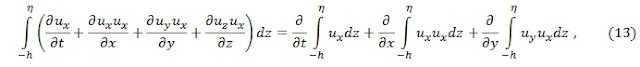



No comments:
Post a Comment