Навиер-Стокесийн тэгшитгэлийн Латтис Больцманы ВГК загвар
Lattice Boltzmann BGK
Model for NS equation
Боловсруулсан: Др Чен Мин
Танилцуулга
Латтис Больцманы арга (Lattice Boltzmann method – LBM, монгол товчлол ЛБА)
нь Навиер-Стокесийн тэгшитгэлийг шийдвэрлэх тооцон бодох шингэний
динамикийн нэгэн хувилбарт арга болж хөгжиж байна. Уламжлалт тоон аргуудтай
адилгүйгээр ЛБА нь хурд, нягт гэх мэт макро-орчны хэмжигдэхүүнүүдийг
шийдвэрлэдэг. ЛБА нь эгэл хэсгүүдийн түгэлтийн функцаар илэрхийлэгдэх макро-орчны
кинетик тэгшитгэл дээр суурилдаг. Макро-орчны тоо хэмжээнүүд нь түгэлтийн
функцын дагуу авсан моментийн интеграцаас олдох боломжтой байдаг.
Тооцон
бодох шингэний динамикт хэрэглэхээр Др Чен ба түүний багийнхан дотоод судалгааны оролдлогууд дээрээ суурилж ЛБА-ын тооцон бодох бүлэг кодийг
хөгжүүлсэн байна. Энэ бүлэг кодоос LBM_D3Q19
фортран код нь Сүлжээний ВГК схемийн энгийн боловсруулалтыг хэрэглэсэн ба
шингэн-хатуу биеийн харилцан үйлчлэлийн бодлогийг шийдвэрлэх зорилготой юм.
Үндсэн алгоритм
Физик
орон зай нь дүрмийн сүлжээнд хуваагдах ба хурдны орон нь төгсгөлөг утгатай хурд {calpha} – аар тухайлагдсан дискрет орчинг бий
болгоно. Энэ нөхцөлд ВГК ойролцоолол бүхий Больцманы тэгшитгэл нь дараах
байдлаар тухайлагдана.
Үүнд: delta t ба calpha*delta
t нь хугацаа ба орон зайн өсөлт юм. galpha
нь alpha чиглэлийн дагуух
түгэлтийн функцын дан-эгэл хэсгийн хурд юм. galphaeq нь
түгэлтийн функцийг тэнцвэржүүлэгч, thau
нь дан сулралтын (тайвшрах) хугацаа юм.
ЛБА-д өөр өөр
төрлийн сүлжээнүүдийг хэрэглэдэг ба сүлжээний төрлөөр нь бас ангилдаг. Олон
зүйл нуршилгүй энгийн байдлаар тайлбарлавал бид доорх зурагт
үзүүлсэнээр D3Q19 гэсэн
загварыг авч үзэж байгаа ба энэ нь 19 хурд бүхий, 3D хэмжээст
квадрат сүлжээ юм.
Зураг 1. D3Q19 загвар
Дулааны
урсгалтэй шингэний хувьд,
D3Q19 загвар дахь түгэлтийн функцын тэнцвэржүүлэгч нь дараах байдлаар өгөгдөнө.
Үүнд:
Макро-орчны
нягт rho болон
хурд u нь дараах
байдлаар төгсгөлөг хурд болон түгэлтийн функцтай холбогдоно.
Чапман-Энсокийн задаргааг ашиглаж тэгшитгэл (1) – ээс хоёрдугаар
эрэмбийн тохиролтой Навиер-Стокесийн тэгшитгэлийг гаргаж авч болох ба энэ
үед кинематик зунгааралт нь доорхи
байдлаар өгөгдөнө.
Стандарт
ЛБА-д тэгшитгэл (1) нь
дараах хоёр шат процесстой байна:
урсгал ба мөргөлдөөн.
Иймд тэгшитгэл (1) тус хоёр
алхамд дараах байддлаар бодогдоно.
Мөргөлдөөн:
Урсгал:
ЛБА тухай илүү дэлгэрэнгүйг Sauro Succi зохиогчтой The Lattice Boltzmann Equation for
Fluid Dynamics and Beyond, Oxford University Press (2001) гэсэн номноос
уншаарай.
Хязгаарын болон Анхны нөхцлүүд
Тооцон бодох
бодлогийн хүрээ нь хайрцаг хэлбэртэй байх ба хэмжээс нь тус бүр XMAX-YMAX-ZMAX байна.
Рейнольдсын тоо нь
Үүнд LN нь характерийн /бодлогийн
геометрийг илэрхийлж чадахуйц уртын хэмжээс/ урт ба v нь тэгшитгэл (5) –
аар өгөгдсөн кинематик зунгааралт юм. Хязгаарын
нөхцөл нь үл гулсах нөхцөлтэйгээр хатуу хананд өгөгдөх ба энэ хэсэгт бүх хурд
үгүй болно. Энэ нь Латтис Больцманы аргад буцаж-ойх дүрмээр боловсруулагдах ба
энэ дүрэмд ханыг мөргөж байгаа эгэл хэсгүүд буцаж ирсэн зүгрүүгээ ойх ёстой.
Жишээлбэл бидний бодлогын хувьд ёроолын хязгаарын нөхцөл нь:
In-state: g0, g1, g2, g3,
g4, g5, g6,
g7, g8, g9,
g10, g11, g12,
g13, g14, g15,
g16, g17, g18
Out-state: g0, g1, g2, g3,
g4, g6, g5,
g7, g8, g9,
g10, g11, g13,
g12, g14, g18,
g17, g16, g15
Оролтын хэсэг
дахь хязгаарын нөхцөл нь дараах байдлаар илэрхийлэгдэнэ.
Фортран кодийн бүтэц
Програмын код нь
үндсэндээ input.dat
болон LBM_D3Q19.f гэсэн файлуудаас бүрдэнэ.
Input.dat бол зарим
параметрүүдийн утгыг өгөхөд хэрэглэгдэнэ. Дараах параметрүүд бол квадрат
хайрцаган дахь урсгалыг симуляци хийх параметрүүд юм.
TMAX= Итерацийн хамгийн их тоо 2001
XMAX= х тэнхлэгийн дагуу торны хэмжээ 41
YMAX= у тэнхлэгийн дагуу торны хэмжээ 41
ZMAX= z тэнхлэгийн дагуу торны хэмжээ
41
NUMAX= Үр дүнг хэвлэх давтамж 1000
U0= Оролтын хэсгийн хурд (U0 < 0.1) 0.02
LBM_D3Q19.f нь 7 ширхэг дэд
програмтай.
wall_coordinate Хатуу хананы координатыг оруулах
init_density нягтын түгэлтийн n функцыг тэнвэржүүлэгчтэй эхлүүлэх
velocity_bc Хурдны хязгаарын нөхцлийг тохируулах
streaming шингэний
нягтыг тэдгээрийн дараачийн хөрш зангилааруу түгээх
bounceback Шингэний нягтууд эргэлдэх хөдөлгөөнд байна. Дараагийн
түгэлтийн шатанд хязгаар орчмын нягтууд буцаж ойх болно.
collision Дан алхамт
нягтуудын мөргөлдөөний процесс
write_results Үр дүнг 'T100XXX.dat' файлаар хэвлэх
T100XXX.dat файлын формат
VARIABLES = X, Y, Z, U, V, W, PRESS
ZONE I=
41, J= 41, K= 41, F=POINT
1
1 1 0.000000E+00 0.000000E+00 0.000000E+00 0.333333E+00
2 1 1 0.000000E+00 0.000000E+00 0.000000E+00 0.333333E+00
3 1 1 0.000000E+00
0.000000E+00 0.000000E+00 0.333333E+00
4 1 1
0.000000E+00 0.000000E+00 0.000000E+00 0.333333E+00
5 1 1
0.000000E+00 0.000000E+00 0.000000E+00 0.333333E+00
X Y
Z Ux
Uy Uz P
Үүнд:
I
х тэнхлэг дахь торны хэмжээ
J
y тэнхлэг дахь торны хэмжээ
X
x координат
Y
y координат
Z
z координат
Ux
х чиглэл дахь хурд
Uy
y чиглэл дахь хурд
Uz
z чиглэл дахь хурд
P
даралт
T100XXX.dat
файлууд нь
TECPLOT програмаар
уншигдана /нээгдэнэ/.
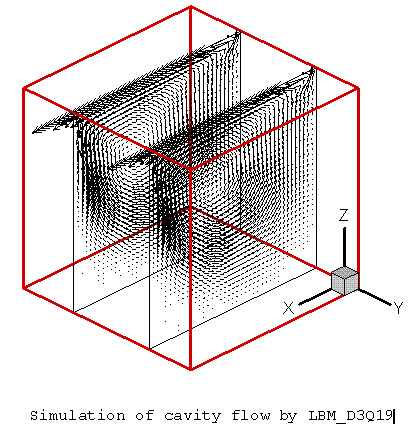 |
| Симуляцийн үр дүн "Хөндийн" урсгалын жишээ |
Видео үр дүн
Фортран код
1. Input.dat
1: TMAX= Maximum number of iterations
2: 80001
3: XMAX = Grid size in x dimension
4: 41
5: YMAX = Grid size in y dimension
6: 41
7: ZMAX = Grid size in z dimension
8: 41
9: NUMAX = Output frequency
10: 1000
11: U0 = Incoming velocity (U0 < 0.1)
12: 0.02
2. Үндсэн код LBM_D3Q19.f
1: c File : LBM_D3Q19.f
2: c Author : Cheng Ming (chengm@ihpc.a-star.edu.sg)
3: c Date : 25-010-2006
4: c Revision : 1.0
5: c DESCRIPTION
6: c This is a Fortan 77 LBM_D3Q19 code for 3D viscous incompressible flow
7: PROGRAM LBM3D
8: c Varibles and parameters
9: implicit none
10: ! XMAX,YMAX.ZMAX.grid size in x y dimension
11: integer XMAX,YMAX,ZMAX,NSTART,NUMB,NPLUS,NUMAX
12: ! density........fluid density per link
13: real*8 density ! *8 is same as double precision
14: ! omega............collision2 parameter
15: real*8 omega
16: ! TMAX.....maximum number of iterations
17: integer TMAX
18: ! time................iteration counter
19: integer time
20: ! obst(81,81,81)........obstacle array
21: logical obst(81,81,81)
22: ! g(0:18,81,81,81)......fluid densities
23: real*8 g(0:18,81,81,81)
24: ! gprop...rray of temporareYMAX storage
25: real*8 gprop(0:18,81,81,81)
26: ! vel............mean velocity computed
27: real*8 vel,Re
28: REAL*8 UW
29: ! ==================================================================
30: ! | Begin initialisation |
31: ! ==================================================================
32: ! Input calculation parameter
33: OPEN(30,file='input0.dat')
34: read(30,*)
35: read(30,*) TMAX
36: read(30,*)
37: read(30,*) XMAX
38: read(30,*)
39: read(30,*) YMAX
40: read(30,*)
41: read(30,*) ZMAX
42: read(30,*)
43: read(30,*) NUMAX
44: read(30,*)
45: read(30,*) UW
46: density=1.0d0
47: ! omega.....................collision2 parameter
48: omega=1.85
49: ! read obstacle
50: call wall_coordinate(obst,XMAX,YMAX,ZMAX)
51: ! initialize lattice velocity
52: call init_density(XMAX,YMAX,ZMAX,density,g)
53: Re=UW*XMAX*3.0/(1.0/omega-0.5)
54: PRINT*,'RE=',Re
55: ! mean sqaure flow is stored in file
56: ! ==================================================================
57: ! | End initialisation |
58: ! ==================================================================
59: ! ==================================================================
60: ! | Begin iterations |
61: ! ==================================================================
62: NSTART=1
63: 1 NUMB =1
64: do time = NSTART, TMAX
65: IF (NUMB.LE.NUMAX) THEN
66: NUMB=NUMB+1
67: END IF
68: ! velocity boundary condition
69: call velocity_bc(density,UW,XMAX,YMAX,ZMAX,g)
70: ! density propagation
71: call streaming(XMAX,YMAX,ZMAX,g,gprop)
72: ! bounc back from obstacles
73: call bounceback(XMAX,YMAX,ZMAX,obst,g,gprop)
74: ! density collision2
75: call collision(density,omega,XMAX,YMAX,ZMAX,g,gprop,obst)
76: ! each TMAX/10 iteration
77: if (NUMB.GT.NUMAX) then
78: ! output results
79: call write_results(XMAX,YMAX,ZMAX,obst,g,density,time,NUMAX,UW)
80: NUMB=1
81: end if
82: end do
83: ! ==================================================================
84: ! | End iterations |
85: ! ==================================================================
86: close(10)
87: end
88: ! ****************************************************************
89: ! * *
90: ! * No obstacles coordinates of a driven cavity flow *
91: ! * *
92: ! ****************************************************************
93: subroutine wall_coordinate(obst,XMAX,YMAX,ZMAX)
94: implicit none
95: integer XMAX,YMAX,ZMAX
96: logical obst(81,81,81)
97: ! local variables
98: integer x,y,z
99: do y = 1, YMAX
100: do x = 1, XMAX
101: do z = 1, ZMAX
102: obst(x,y,z) = .false.
103: end do
104: end do
105: end do
106: DO x=1, XMAX
107: DO z=1, ZMAX
108: obst(x,1 ,z)= .true.
109: obst(x,YMAX,z)= .true.
110: END DO
111: END DO
112: DO x=1, XMAX
113: DO y=1, YMAX
114: obst(x,y,1)= .true.
115: END DO
116: END DO
117: DO y=1, YMAX
118: DO z=1, ZMAX
119: obst(1 ,y,z)= .true.
120: obst(XMAX,y,z)= .true.
121: END DO
122: END DO
123: END
124: ! ****************************************************************
125: ! * *
126: ! * Initialize density distribution function n with equilibrium *
127: ! * for zero velocity *
128: ! * *
129: ! ****************************************************************
130: subroutine init_density(XMAX,YMAX,ZMAX,density,g)
131: implicit none
132: integer XMAX,YMAX,ZMAX
133: real*8 density,g(0:18,81,81,81)
134: ! local variables
135: integer x,y,z
136: real*8 t0,t1,t2
137: ! compute weighting factors (depending on lattice geometry)
138: t0 = density / 3.0d0
139: t1 = density / 18.d0
140: t2 = density / 36.d0
141: ! z=1
142: ! y=1
143: ! loop over computational domain
144: do x = 1, XMAX
145: do y = 1, YMAX
146: DO z = 1, ZMAX
147: g(0,x,y,z) =t0
148: g(1,x,y,z) =t1
149: g(2,x,y,z) =t1
150: g(3,x,y,z) =t1
151: g(4,x,y,z) =t1
152: g(5,x,y,z) =t1
153: g(6,x,y,z) =t1
154: g(7,x,y,z) =t2
155: g(8,x,y,z) =t2
156: g(9,x,y,z) =t2
157: g(10,x,y,z)=t2
158: g(11,x,y,z)=t2
159: g(12,x,y,z)=t2
160: g(13,x,y,z)=t2
161: g(14,x,y,z)=t2
162: g(15,x,y,z)=t2
163: g(16,x,y,z)=t2
164: g(17,x,y,z)=t2
165: g(18,x,y,z)=t2
166: END DO
167: end do
168: end do
169: end
170: ! ****************************************************************
171: ! * *
172: ! * Velocity bounday condition *
173: ! * *
174: ! ****************************************************************
175: subroutine velocity_bc(density,UW,XMAX,YMAX,ZMAX,g)
176: implicit none
177: integer XMAX,YMAX,ZMAX
178: real*8 density,g(0:18,81,81,81),UW
179: integer x,y,z,i
180: real*8 C1,C2,C3,t0,t1,t2,U,V,W,un(18),usqu,d_loc
181: real*8 dt0,dt1,dt2
182: t0 = 1.d0 / 3.d0
183: t1 = 1.d0 / 18.d0
184: t2 = 1.d0 / 36.d0
185: ! square speed of sound
186: C1 = 1.d0 / 3.d0
187: C2 = 2.d0 * C1 ** 2.d0
188: C3 = 2.d0 * C1
189: d_loc = density
190: dt0=t0*d_loc
191: dt1=t1*d_loc
192: dt2=t2*d_loc
193: ! z=1
194: ! y=1
195: ! y = YMAX
196: z = ZMAX
197: do x = 1, XMAX
198: do y = 1, YMAX
199: U = UW
200: V = 0.0d0
201: W = 0.0d0
202: usqu = (U * U + V * V + W * W)/C3
203: un(1) = U
204: un(2) = -U
205: un(3) = V
206: un(4) = - V
207: un(5) = W
208: un(6) = - W
209: un(7) = U + V
210: un(8) = U - V
211: un(9) = - U + V
212: un(10)= - U - V
213: un(11)= U + W
214: un(12)= - U + W
215: un(13)= U - W
216: un(14)= - U - W
217: un(15)= V + W
218: un(16)= V - W
219: un(17)= - V + W
220: un(18)= - V - W
221: g(0, x,y,z)=dt0*(1.d0 -usqu)
222: g(1, x,y,z)=dt1*(1.d0+un( 1)/C1+un( 1)**2.d0/C2-usqu)
223: g(2, x,y,z)=dt1*(1.d0+un( 2)/C1+un( 2)**2.d0/C2-usqu)
224: g(3, x,y,z)=dt1*(1.d0+un( 3)/C1+un( 3)**2.d0/C2-usqu)
225: g(4, x,y,z)=dt1*(1.d0+un( 4)/C1+un( 4)**2.d0/C2-usqu)
226: g(5, x,y,z)=dt1*(1.d0+un( 5)/C1+un( 5)**2.d0/C2-usqu)
227: g(6, x,y,z)=dt1*(1.d0+un( 6)/C1+un( 6)**2.d0/C2-usqu)
228: g(7, x,y,z)=dt2*(1.d0+un( 7)/C1+un( 7)**2.d0/C2-usqu)
229: g(8, x,y,z)=dt2*(1.d0+un( 8)/C1+un( 8)**2.d0/C2-usqu)
230: g(9, x,y,z)=dt2*(1.d0+un( 9)/C1+un( 9)**2.d0/C2-usqu)
231: g(10,x,y,z)=dt2*(1.d0+un(10)/C1+un(10)**2.d0/C2-usqu)
232: g(11,x,y,z)=dt2*(1.d0+un(11)/C1+un(11)**2.d0/C2-usqu)
233: g(12,x,y,z)=dt2*(1.d0+un(12)/C1+un(12)**2.d0/C2-usqu)
234: g(13,x,y,z)=dt2*(1.d0+un(13)/C1+un(13)**2.d0/C2-usqu)
235: g(14,x,y,z)=dt2*(1.d0+un(14)/C1+un(14)**2.d0/C2-usqu)
236: g(15,x,y,z)=dt2*(1.d0+un(15)/C1+un(15)**2.d0/C2-usqu)
237: g(16,x,y,z)=dt2*(1.d0+un(16)/C1+un(16)**2.d0/C2-usqu)
238: g(17,x,y,z)=dt2*(1.d0+un(17)/C1+un(17)**2.d0/C2-usqu)
239: g(18,x,y,z)=dt2*(1.d0+un(18)/C1+un(18)**2.d0/C2-usqu)
240: end do
241: end do
242: end
243: ! ****************************************************************
244: ! * *
245: ! * streaming2 fluid densities to their next neighbour nodes *
246: ! * *
247: ! ****************************************************************
248: subroutine streaming(XMAX,YMAX,ZMAX,g,gprop)
249: implicit none
250: integer XMAX,YMAX,ZMAX
251: real*8 g(0:18,81,81,81),gprop(0:18,81,81,81)
252: integer x,y,z,x_e,x_w,y_n,y_s,z_t,z_b
253: ! z=1
254: ! y=1
255: do x = 1, XMAX
256: do y = 1, YMAX
257: do z = 1, ZMAX
258: x_e = mod(x,XMAX) + 1
259: y_n = mod(y,YMAX) + 1
260: z_t = mod(z,ZMAX) + 1
261: x_w = XMAX - mod(XMAX + 1 - x, XMAX)
262: y_s = YMAX - mod(YMAX + 1 - y, YMAX)
263: z_b = ZMAX - mod(ZMAX + 1 - z, ZMAX)
264: gprop( 0, x , y , z ) = g( 0,x,y,z)
265: gprop( 1, x_e, y , z ) = g( 1,x,y,z)
266: gprop( 2, x_w, y , z ) = g( 2,x,y,z)
267: gprop( 3, x , y_n, z ) = g( 3,x,y,z)
268: gprop( 4, x , y_s, z ) = g( 4,x,y,z)
269: gprop( 5, x , y , z_t) = g( 5,x,y,z)
270: gprop( 6, x , y , z_b) = g( 6,x,y,z)
271: gprop( 7, x_e, y_n, z ) = g( 7,x,y,z)
272: gprop( 8, x_e, y_s, z ) = g( 8,x,y,z)
273: gprop( 9, x_w, y_n, z ) = g( 9,x,y,z)
274: gprop(10, x_w, y_s, z ) = g(10,x,y,z)
275: gprop(11, x_e, y , z_t) = g(11,x,y,z)
276: gprop(12, x_w, y , z_t) = g(12,x,y,z)
277: gprop(13, x_e, y , z_b) = g(13,x,y,z)
278: gprop(14, x_w, y , z_b) = g(14,x,y,z)
279: gprop(15, x , y_n, z_t) = g(15,x,y,z)
280: gprop(16, x , y_n, z_b) = g(16,x,y,z)
281: gprop(17, x , y_s, z_t) = g(17,x,y,z)
282: gprop(18, x , y_s, z_b) = g(18,x,y,z)
283: end do
284: end do
285: end do
286: end
287: ! ****************************************************************
288: ! * *
289: ! * Fluid densities are rotated. By the next propagation step, *
290: ! * this results in a bounce back from obstacle nodes. *
291: ! * *
292: ! ****************************************************************
293: subroutine bounceback(XMAX,YMAX,ZMAX,obst,g,gprop)
294: implicit none
295: integer XMAX,YMAX,ZMAX
296: logical obst(81,81,81)
297: real*8 g(0:18,81,81,81),gprop(0:18,81,81,81)
298: ! local variables
299: integer x,y,z
300: ! z=1
301: ! y=1
302: do x = 1, XMAX
303: do y = 1, YMAX
304: do z = 1, ZMAX
305: if (obst(x,y,z)) then
306: g( 1, x,y,z) = gprop( 2, x,y,z)
307: g( 2, x,y,z) = gprop( 1, x,y,z)
308: g( 3, x,y,z) = gprop( 4, x,y,z)
309: g( 4, x,y,z) = gprop( 3, x,y,z)
310: g( 5, x,y,z) = gprop( 6, x,y,z)
311: g( 6, x,y,z) = gprop( 5, x,y,z)
312: g( 7, x,y,z) = gprop(10, x,y,z)
313: g( 8, x,y,z) = gprop( 9, x,y,z)
314: g( 9, x,y,z) = gprop( 8, x,y,z)
315: g(10, x,y,z) = gprop( 7, x,y,z)
316: g(11, x,y,z) = gprop(14, x,y,z)
317: g(12, x,y,z) = gprop(13, x,y,z)
318: g(13, x,y,z) = gprop(12, x,y,z)
319: g(14, x,y,z) = gprop(11, x,y,z)
320: g(15, x,y,z) = gprop(18, x,y,z)
321: g(16, x,y,z) = gprop(17, x,y,z)
322: g(17, x,y,z) = gprop(16, x,y,z)
323: g(18, x,y,z) = gprop(15, x,y,z)
324: end if
325: end do
326: end do
327: end do
328: end
329: ! ****************************************************************
330: ! * *
331: ! * One-step density collision2 process *
332: ! * *
333: ! ****************************************************************
334: subroutine collision(density,omega,XMAX,YMAX,ZMAX,g,gprop,obst)
335: implicit none
336: integer XMAX,YMAX,ZMAX
337: logical obst(81,81,81)
338: real*8 density,omega,g(0:18,81,81,81),gprop(0:18,81,81,81)
339: ! local variables
340: integer x,y,z,i
341: real*8 C1,C2,C3,t0,t1,t2,U,V,W,un(18),gq(0:18),usqu,d_loc
342: real*8 dt0,dt1,dt2,omega1
343: t0 = 1.d0 / 3.d0
344: t1 = 1.d0 / 18.d0
345: t2 = 1.d0 / 36.d0
346: C1 = 1.d0 / 3.d0
347: C2 = 2.d0 * C1 ** 2.d0
348: C3 = 2.d0 * C1
349: t0 = omega*t0
350: t1 = omega*t1
351: t2 = omega*t2
352: omega1=1.0d0-omega
353: ! z=1
354: ! y=1
355: do x = 1, XMAX
356: do y = 1, YMAX
357: do z = 1, ZMAX
358: ! only free nodes are considered here
359: if (.not. obst(x,y,z)) then
360: ! calculate local density d_loc
361: d_loc = gprop( 0, x,y,z)
362: & + gprop( 1, x,y,z) + gprop( 2, x,y,z)
363: & + gprop( 3, x,y,z) + gprop( 4, x,y,z)
364: & + gprop( 5, x,y,z) + gprop( 6, x,y,z)
365: & + gprop( 7, x,y,z) + gprop( 8, x,y,z)
366: & + gprop( 9, x,y,z) + gprop(10, x,y,z)
367: & + gprop(11, x,y,z) + gprop(12, x,y,z)
368: & + gprop(13, x,y,z) + gprop(14, x,y,z)
369: & + gprop(15, x,y,z) + gprop(16, x,y,z)
370: & + gprop(17, x,y,z) + gprop(18, x,y,z)
371: ! d_loc = density
372: ! calculate velocity components
373: U = gprop(1 , x,y,z) - gprop( 2, x,y,z)
374: & + gprop(7 , x,y,z) + gprop( 8, x,y,z)
375: & - gprop(9 , x,y,z) - gprop(10, x,y,z)
376: & + gprop(11, x,y,z) - gprop(12, x,y,z)
377: & + gprop(13, x,y,z) - gprop(14, x,y,z)
378: U = U / d_loc
379: V = gprop( 3, x,y,z) - gprop( 4, x,y,z)
380: & + gprop( 7, x,y,z) - gprop( 8, x,y,z)
381: & + gprop( 9, x,y,z) - gprop(10, x,y,z)
382: & + gprop(15, x,y,z) + gprop(16, x,y,z)
383: & - gprop(17, x,y,z) - gprop(18, x,y,z)
384: V = V / d_loc
385: W = gprop( 5, x,y,z) - gprop( 6, x,y,z)
386: & + gprop(11, x,y,z) + gprop(12, x,y,z)
387: & - gprop(13, x,y,z) - gprop(14, x,y,z)
388: & + gprop(15, x,y,z) - gprop(16, x,y,z)
389: & + gprop(17, x,y,z) - gprop(18, x,y,z)
390: W = W / d_loc
391: usqu = (U * U + V * V + W*W)/C3
392: un( 1) = U
393: un( 2) = -U
394: un( 3) = V
395: un( 4) = - V
396: un( 5) = W
397: un( 6) = - W
398: un( 7) = U + V
399: un( 8) = U - V
400: un( 9) = - U + V
401: un(10) = - U - V
402: un(11) = U + W
403: un(12) = - U + W
404: un(13) = U - W
405: un(14) = - U - W
406: un(15) = V + W
407: un(16) = V - W
408: un(17) = - V + W
409: un(18) = - V - W
410: dt0=t0*d_loc
411: dt1=t1*d_loc
412: dt2=t2*d_loc
413: gq( 0) =dt0*(1.d0 -usqu)
414: gq( 1)= dt1*(1.d0+un( 1)/C1+un( 1)**2.d0/C2-usqu)
415: gq( 2)= dt1*(1.d0+un( 2)/C1+un( 2)**2.d0/C2-usqu)
416: gq( 3)= dt1*(1.d0+un( 3)/C1+un( 3)**2.d0/C2-usqu)
417: gq( 4)= dt1*(1.d0+un( 4)/C1+un( 4)**2.d0/C2-usqu)
418: gq( 5)= dt1*(1.d0+un( 5)/C1+un( 5)**2.d0/C2-usqu)
419: gq( 6)= dt1*(1.d0+un( 6)/C1+un( 6)**2.d0/C2-usqu)
420: gq( 7)= dt2*(1.d0+un( 7)/C1+un( 7)**2.d0/C2-usqu)
421: gq( 8)= dt2*(1.d0+un( 8)/C1+un( 8)**2.d0/C2-usqu)
422: gq( 9)= dt2*(1.d0+un( 9)/C1+un( 9)**2.d0/C2-usqu)
423: gq(10)= dt2*(1.d0+un(10)/C1+un(10)**2.d0/C2-usqu)
424: gq(11)= dt2*(1.d0+un(11)/C1+un(11)**2.d0/C2-usqu)
425: gq(12)= dt2*(1.d0+un(12)/C1+un(12)**2.d0/C2-usqu)
426: gq(13)= dt2*(1.d0+un(13)/C1+un(13)**2.d0/C2-usqu)
427: gq(14)= dt2*(1.d0+un(14)/C1+un(14)**2.d0/C2-usqu)
428: gq(15)= dt2*(1.d0+un(15)/C1+un(15)**2.d0/C2-usqu)
429: gq(16)= dt2*(1.d0+un(16)/C1+un(16)**2.d0/C2-usqu)
430: gq(17)= dt2*(1.d0+un(17)/C1+un(17)**2.d0/C2-usqu)
431: gq(18)= dt2*(1.d0+un(18)/C1+un(18)**2.d0/C2-usqu)
432: g( 0, x,y,z) = omega1*gprop( 0, x,y,z)+gq( 0)
433: g( 1, x,y,z) = omega1*gprop( 1, x,y,z)+gq( 1)
434: g( 2, x,y,z) = omega1*gprop( 2, x,y,z)+gq( 2)
435: g( 3, x,y,z) = omega1*gprop( 3, x,y,z)+gq( 3)
436: g( 4, x,y,z) = omega1*gprop( 4, x,y,z)+gq( 4)
437: g( 5, x,y,z) = omega1*gprop( 5, x,y,z)+gq( 5)
438: g( 6, x,y,z) = omega1*gprop( 6, x,y,z)+gq( 6)
439: g( 7, x,y,z) = omega1*gprop( 7, x,y,z)+gq( 7)
440: g( 8, x,y,z) = omega1*gprop( 8, x,y,z)+gq( 8)
441: g( 9, x,y,z) = omega1*gprop( 9, x,y,z)+gq( 9)
442: g(10, x,y,z) = omega1*gprop(10, x,y,z)+gq(10)
443: g(11, x,y,z) = omega1*gprop(11, x,y,z)+gq(11)
444: g(12, x,y,z) = omega1*gprop(12, x,y,z)+gq(12)
445: g(13, x,y,z) = omega1*gprop(13, x,y,z)+gq(13)
446: g(14, x,y,z) = omega1*gprop(14, x,y,z)+gq(14)
447: g(15, x,y,z) = omega1*gprop(15, x,y,z)+gq(15)
448: g(16, x,y,z) = omega1*gprop(16, x,y,z)+gq(16)
449: g(17, x,y,z) = omega1*gprop(17, x,y,z)+gq(17)
450: g(18, x,y,z) = omega1*gprop(18, x,y,z)+gq(18)
451: end if
452: end do
453: end do
454: end do
455: end
456: ! ****************************************************************
457: ! * *
458: ! * Output of rsults to file 'result.dat' *
459: ! * *
460: ! ****************************************************************
461: subroutine write_results(XMAX,YMAX,ZMAX,obst,g,density
462: & ,time,NUMAX,UW)
463: implicit none
464: integer XMAX,YMAX,ZMAX,time,NUMAX
465: real*8 g(0:18,81,81,81),density,UW
466: logical obst(81,81,81)
467: ! local variables
468: integer x,y,z,i
469: real*8 U,V,W,d_loc,press,c_squ
470: CHARACTER *6 rr
471: ! square speed of sound
472: c_squ = 1.d0 / 3.d0
473: ! open results output file
474: cccccc rr=character(time)
475: print*,'time=',time
476: WRITE (rr,200) 100000+time/NUMAX
477: 200 FORMAT (I6)
478: open(11,file='T'//TRIM(rr)//'.dat')
479: !
480: ! write header for postprocessing with TECPLOT
481: write(11,*) 'VARIABLES = X, Y, Z, U, V, W, PRESS'
482: write(11,*) 'ZONE I=',XMAX,', J=', YMAX,', K=',ZMAX,', F=POINT'
483: ! y=20
484: do z = 1, ZMAX
485: do y = 1, YMAX
486: do x = 1, XMAX
487: ! if obstacle node, nothing is to do
488: if (obst(x,y,z)) then
489: ! velocity components = 0
490: U = 0.d0
491: V = 0.d0
492: W = 0.d0
493: ! pressure = average pressure
494: press = density * c_squ
495: else
496: ! calculate local density d_loc
497: d_loc = g( 0,x,y,z)
498: & + g( 1,x,y,z) + g( 2,x,y,z)
499: & + g( 3,x,y,z) + g( 4,x,y,z)
500: & + g( 5,x,y,z) + g( 6,x,y,z)
501: & + g( 7,x,y,z) + g( 8,x,y,z)
502: & + g( 9,x,y,z) + g(10,x,y,z)
503: & + g(11,x,y,z) + g(12,x,y,z)
504: & + g(13,x,y,z) + g(14,x,y,z)
505: & + g(15,x,y,z) + g(16,x,y,z)
506: & + g(17,x,y,z) + g(18,x,y,z)
507: U = g( 1,x,y,z) - g(2, x,y,z)
508: & + g( 7,x,y,z) + g(8, x,y,z)
509: & - g( 9,x,y,z) - g(10,x,y,z)
510: & + g(11,x,y,z) - g(12,x,y,z)
511: & + g(13,x,y,z) - g(14,x,y,z)
512: U = U/ d_loc
513: V = g( 3,x,y,z) - g( 4,x,y,z)
514: & + g( 7,x,y,z) - g( 8,x,y,z)
515: & + g( 9,x,y,z) - g(10,x,y,z)
516: & + g(15,x,y,z) + g(16,x,y,z)
517: & - g(17,x,y,z) - g(18,x,y,z)
518: V = V/ d_loc
519: W = g( 5,x,y,z) - g( 6,x,y,z)
520: & + g(11,x,y,z) + g(12,x,y,z)
521: & - g(13,x,y,z) - g(14,x,y,z)
522: & + g(15,x,y,z) - g(16,x,y,z)
523: & + g(17,x,y,z) - g(18,x,y,z)
524: W = W/ d_loc
525: ! calculate pressure
526: press = d_loc * c_squ
527: end if
528: if (z.eq.ZMAX) then
529: U = UW
530: V = 0.0d0
531: W = 0.0d0
532: press = density * c_squ
533: end if
534: ! write results to file
535: write(11,100) x,y,z,U,V,W, press
536: 100 format(3I8,4E15.6)
537: end do
538: end do
539: end do
540: ! close file 'result.dat'
541: close(11)
542: end








No comments:
Post a Comment