ШУТИС-т байхад санаандгүйгээр бас гол гаргах маягаар задгай голдиролийн гидравликтай холбоотой хэд хэдэн англи номтой болсон юм. Эдгээр номонд гидравлик загварчлалын хэсэгт турбулент урсгалын маш олон загварчлалын тухай, хүйтэн хүйтэн төрхтэй олон дифференциал тэгшитгэлүүдтэй загварууд олон байдаг ч уншаад ойлгох нь ховор байваа. Тэдгээрийн нэг болох олон удаа өлийн даваан дээр дайралдаж байсан нөхөр бол яах аргагүй доор дурьдах К-Эпсилон загвар юм.
К-Эпсилон загвар
К-Эпсилон загвар
нь ихээхэн даралтын өөрчлөлттэй урсгалд сайн тохирдоггүй боловч хамгийн
түгээмэл хэрэглэгддэг турбулент загварчлалын нэг юм. энэ бол хоёр тэгшитгэлт
загвар бөгөөд энэ тэгшитгэлүүд нь шингэний урсгалын турбулент шинж чанарт
нэмэлт зөөгдөлт/шилжилтийн тэгшитгэлийг хамааруулж үзнэ. Эдгээр хоёр тэгшитгэл
нь тунбулент энергийн тархалт, конвекци гэх мэт хугацаанаас хамаарсан нөлөөллийг
тооцох юм. Эхний шилжихүйц, тээвэрлэгдэхүйц хэмжигдэхүүн нь турбулент кинетик
энерги k юм.
Хоёр дахь
тээвэрлэгдэхүйц хэмжигдэхүүн нт турбулент тархалтын утга epsilon юм. энергийн сарнилтын утга нь
турбулентийн хэмжигдэхүүний тодорхойлох бол турбулент кинетик энерги нь
турбулент урсгал дахь энергийг тодорхойлно. К-Эпсилон загварыг илэрхийлэх хэд
хэдэн аргачлал байх ба ерөнхийд нь хоёр үндсэн аргачлал байна гэж үздэг. Үүнээс
Лаундер болон Шарма нарын боловсруулсан аргыг стандарт К-Эпсилон загвар гэж
нэрлэдэг. К-эпсилон загварын үндсэн хөшүүрэг нь холилдох уртын загварыг
сайжруулах мөн маш төвөгшилтэй урсгалыг зохицуулахад турбулент уртын хэмжээсийг
тайлбарлах алгебрийн хувилбарыг тодорхойлох гэх мэт байсан юм. Лавлахуудад
дурьдсанаар К-эпсилон загвар нь харьцангуй бага даралтын градиенттай чөлөөт
шүргэх үеийн урсгалын хувьд тохиромжтой байна гэжээ. Үүнтэй адилаар дотоод урсгал болон
ханаар хүрээлэгдсэн урсгалын хувьд энэхүү загвар нь мөн л дундаж даралтын
градиент нь бага тохиолдолд чанартай үр дүнг өгнө. Өөрөөр хэлбэл тооцооллын
нарийвчлал нь даралтын градиент ихтэй бол буурдаг гэдгийг туршилтаар баталжээ.
Иймд бодлогийн оролт гаралт, геометрийн огцом өөрчлөлт гэх мэт бүсэд
тохиромжгүй эсвэл бага тохиролтой байж болно.
Стандарт К-Эпсилон загвар
Эйнштэйний тэмдэглэгээг
ашиглан Навьер-Стокесийн тэгшитгэлийг бичвэл:
Энд байх uu нь Рейнольдсын
хүчдэл гэж нэрлэгдэх ба К-эпислон загварт дараах байдлаар илэрхийлэгдэнэ.
Энд к нь турбулент
кинетик энерги, нют нь турбулент зунгааралт болно. Турбулент
зунгааралтыг илэрхийлэх олон аргачлал байх ба к-эпсилон загварт дараах байдлаар
илэрхийлнэ.
Тэгшитгэл 2-ийн
баруун гар талын хоёр дахь хаалтанд байх илэрхийллийг Sij гэж тэмдэглэж хэв гажилтын утга буюу шүргэх хурд
гэж нэрлэнэ. Тэгшитгэл 4-д байх Смю коэффициент нь тогтмол ба ихэнх
тооцоололд 0.09 гэсэн утгыг авна. Тооцооллыг эхлэхийн тулд турбулент кинетик
энерги болон түүний сарьнилтын утгад эерэг анхны утгуудыг өгөх шаардлагатай.
Салангид төсгөлөг ялгаварын тороор бодлогын геометрийг тухайлсан бол уг хоёр
хэмжигдэхүүн нүдний төвд бодогдоно. Анхны утга авсан бол уг хоёр
хэмжигдэхүүнийг хугацааны алхам бүрд тархалт-конвкцийн тэгшитгэлээр
үргэлжлүүлэн тооцно.
Дээрх тунбулент
энергийн тархалт-конвекцийн тэгшитгэлд байх Pk үржвэрийг хурднаас үүсэлтэй энергийн бүтээгдэхүүн гэж нэрлэх ба
дараах байдлаар тодорхойлно.
Энд S
нь гажих утгын дундаж тенсорын модуль
бөгөөд дараах байдлаар илэрхийлэгдэнэ.
Тархалтын
илэрхийлэлд байх тархалтын коэффициент нь орон зайнаас хамаарсан функц бол
дифференциалын дотор бичигддэг. Турбулент кинематик энерги ба түүний сарьнилтыг
илэрхийлэх тархалтын илэрхийллийн тархалтын коэффициент нь уг хоёр
хэмжигдэхүүнээс хамаарсан турбулент зунгааралтын утгаар илэрхийлэгдэх учир
ямагт дифференциалын дотор байна. Тэгшитгэл 4 ба 5 нь хураангуй хэлбэрээр
өгөгдсөн бол тархалтын илэрхийллийг дараах байдлаар илэрхийлж болно.
Дээрх тэгшитгэлүүд
дахь коэффициентуудыг өгвөл
Зарим тохиолдолд
дээрх тархалт-конвекцийн тэгшитгэл дээр нэмж хөвөлтийн нөлөөг тооцдог ба уг
бүтээгдэхүүнийг дараах байдлаар илэрхийлнэ.
Энд Prt
нь энерги дахь турбулент Прандтлын тоо ба gi
нь i чиглэл дахь хүндийн хүчний хурдатгал. Стандарт болон
биелхүйц к-эпсилон загваруудын хувьд Прандтлын тооны үндсэн утга нь 0.85 байх
ба дулааны тэлэлтийн коэффициентыг дараах байдлаар илэрхийлнэ.
Дээрх тэгшитгэлд
байх хурднууд нь ямар нэгэн шүүлтүүр хэрэглэсэн байх ба уг хурдны жинхэнэ
задаргаа нь жинхэнэ хурд ба хурдны лугшилтын нийлбэрээр тайлбарлагдана.
Figure 1. бодит
ба бодит хурдны лугшилт, дундажилсан хурд
Бодит шингэний
НС-ын тэгшитгэлд дээрх бодит хурдны тайлбарыг орлуулбал хурдны лугшилтаас
үүдэлтэй хүчдэлүүд үүсэх ба үүнийг Рейнольдсын хүчдэл гэж нэрлэдэг байна. Төгсгөлөг ялгаварын аргаар К-Эпсилон загварыг тухайлахад гажих утгын тенсорыг зөв бодох
нь чухал байдаг. Шүүгдсэн буюу дундажилсан хурдын тэмдэглэгээг энгийнээр тэмдэглэвэл:
Тухайлахын өмнө
бутархай торыг (staggered grid) авч үзье.
Figure 2. Бутархай
торны байгуулалт, нүдний хурд ба дундажилсан хурдны байрлал
Тэгшитгэл 13-ийн
тэнцүүгийн тэмдэгийн арын илэрхийллийн эхний гишүүнийг Эйнштэйний
тэмдэглэгээнээс гаргавал:
Иймд 2 хэмжээстэд
i,j=1,2 байхад гажих утгын
тенсор нь дараах хэлбэртэй бичигдэнэ.
Эдгээрийг тэгшитгэл
14-д харуулсан шиг Эйнштэйний тэмдэглэгээнээс тус бүр салган бичвэл:
Дээрхээс S12
ба S21 нь харилцан адил байгаа учир нэгийг нь
бодоход хангалттай. Гурван хэмжээст орчинд 9 ширхэг гишүүнтэй хүчдэлийн тенсор
үүсэх ба тэдгээрийн S21=S12, S31=S13,
S32=S23 нар
харилцан адил байх учир 6 ширхэг хүчдэл бодогдоно.
Хоёр хэмжээстэд
бид S11 S12 S22 гэсэн гурван хүчдэл бодох ба дээрх бутархай торон
дээр дараах байдлаар тухайлагдана.
Figure 3. Дундажилсан
хурдны тодорхойлолт
Тэгшитгэл 17 байх
дундажилсан хурдыг зураг 3-т хэрхэн тодорхойлохыг харуулсан байна. Үүнийг тэгшитгэлээр
бичвэл:
Нэгэнт гажих утгын
хүчдэл 3-н байдлаар тодорхойлогдох учир Рейнольдсын хүчдэл мөн адил тоогоор
тодорхойлогдоно.
Турбулент кинетик
энерги болон түүний сарнилтыг тооцох тархалт-конвекцийн тэгшитгэлүүдийг
нарийвчлалтай бодоход тархалтын гишүүнийг өндөр эрэмбийн тохиролтойгоор
тухайлах шаардлагатай. Ердийн тархалт конвекцийн тэгшитгэлийг жишээ болгон
тухайлъя. Ингээд ердийн байдлаар тэгшитгэлийг бичвэл:
Энэ тэгшитгэлийг цүлхэлтийн
аргаар тухайлбал:
Энд байх
тархалтын коэффициентууд нь зунгааралтаас хамаарсан орон зайн функц учраас
дараах байдлаар тухайлагдана.
Энд ню нь молекул
зунгааралтын коэффициент, нют нь тэгшитгэл 3-аар тодорхойлогдох
турбулент зунгааралтын коэффициент байна. Тэгшитгэл 19-ийн зүүн талын сүүлийн
хоёр адвекцийг тэнцүүгийн тэмдгийн ард гаргаж эсвэл тэгшитгэл 20-ийн хугацааны
дифферениалаас бусад илэрхийллийг тэнцүүгийн тэмдэгийн ард гаргаж бүтээгдэхүүн
болон сарнилтын утга зэргийг хамруулан бичвэл:
Энгийн Эйлэрийн
ялгаварыг ашиглавал
Харин нарийвчлал
болон тооцооллын тогтворшилтыг сайжруулж Адам Вашорфийн олон алхамт шугаман
ялгаварын аргыг хэрэглэвэл:
Энэ тооцооллын үед rh
гэж нэрдэгдэх илэрхийллийн хуучин хугацааны
алхам дахь утгыг хадгалж явах шаардлагатай юм. Харин тэгшитгэол 20-д байх
цүлхэлтүүдийг дараах ялгавараар ойролцоолно.
Анхааруулга: 21-р тэгшитгэл гээд хоёр удаа дугаарласан байна. Үг үсгийн алдаа байгааг үгүйсгэхгүй. Уг загварыг кодолсон фортран эх кодыг сүүлд оруулах болно.





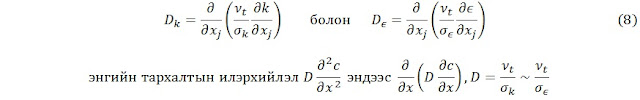















No comments:
Post a Comment