Төгсгөлөг ялгаварын ил арга /Explicit
finite Difference methods/
5.1 Хоёр
түвшний арга /Two-Level
method/
Хэрэв 4.2 хэсэгт байгаатай ижил торны цэгүүд хэрэглэхэд
ямар нэгэн хязгаарлалт байвал ерөнхий ил арга дараах байдлаар бичигдэнэ.
Энд alpha нь тогтворшилт болон нарийвчлалыг залах чөлөөт параметр юм. Энэ бүлэгт байх жишээнд энэ нь задралын илэрхийлэх байхгүй энгийн долгионы тэгшитгэлийг ойролцоолоход ерөнхий арга үнэхээр мөн гэдгийг батлан харуулах болно. Хэрэв alpha=1 бол Лаксийн аргыг хэрэглэх боломж гарна. Тиймээс ерөнхий тохиолдолд үүнийг засварласан Лаксын арга (Modified Lax method) гэнэ. Alpha=0 байх онцгой тохиолдлыг 4.2 хэсэгт хэрэглэсэн болно.
Энд alpha нь тогтворшилт болон нарийвчлалыг залах чөлөөт параметр юм. Энэ бүлэгт байх жишээнд энэ нь задралын илэрхийлэх байхгүй энгийн долгионы тэгшитгэлийг ойролцоолоход ерөнхий арга үнэхээр мөн гэдгийг батлан харуулах болно. Хэрэв alpha=1 бол Лаксийн аргыг хэрэглэх боломж гарна. Тиймээс ерөнхий тохиолдолд үүнийг засварласан Лаксын арга (Modified Lax method) гэнэ. Alpha=0 байх онцгой тохиолдлыг 4.2 хэсэгт хэрэглэсэн болно.
Хязгаарууд нь 4.2 – т хэрэглэсэнтэй адил зарчмаар
шийдэгдэнэ. t=0 үе дахь
анхны нөхцөл өгөгдсөн ба энэ нь тооцон бодоход хүрэлцээтэй нөхцөл байна. Дээд
хашицын хязгаарт x=0 (хэрэв u>0) хязгаарын нөхцөл нь
тооцож авахад боломжтой байна. Доод хашицын хил дээр ямарч хязгаарын нөхцөл
байхааргүй гэх мэт нөхцөл боломжтой бол бид “дээд хэсгийн” ялгаварын тэгшитгэлийг (4.10 тэгшитгэл) хэрэглэж болно.
Энэ аргын тогтворжилтыг судлахад Вон Нeуманны аргыг (Von Neumann) дахин хэрэглэнэ. 4.2 хэсэгтэй ижил хандлагыг хэрэглэж нэмэгдэлтийн
хүчин зүйлийг дараах байдлаар олно.
Үүнд sigma=u*delta t/delta x ба psi=2*pi*delta x/L байна. Хамгийн бага байх боломжит торны хэмжээ мэдээж delta x=0 байх юм. Өөрөөр хэлбэл, Хамгийн их байх боломжит утга нь delta x=L/2 байх ба долгионы уртад хоёроос доош цэгтэй тор хэрэглэж долгионыг харуулна гэдэг байж болошгүй юм. Эсрэгээр, Хамгийн бага боломжит долгионы урт нь 2delta x гэсэн тодорхой торны цэгүүдэд л дүрслэгдэх болно. За ямарч байсан үр дүн нь дараах байдалтай байна.
Харин тогтворжилтын шаардлага нь тэгшитгэл 5.3-д байх бүх л утгын хувьд:
Аятайхан байдлаар 5.4 тэгшитгэлийг сийрүүлбэл
Энэ бол cos psi – ийн шугаман функ байна. Тэгэхээр хэрэв ялгаатай байдал нь хоёр туйлын утга болох +-1 утганд хангалттай байвал энэ нь дундаж утгатай гэсэн үг. Үүнийг бичвэл
Засварласан Лакс-ийн схемд тогтворшилтын нөхцлөөр дээрх хоёрыг нэгтгэн бичвэл:
Үүний утга нь бид alpha болон delta x – ийг сонгож дараа нь 5.5 тэгшитгэлээр хязгаарлагдсан delta t – г сонгож болно гэсэн үг юм. Хугацааны алхамыг дурын байдлаар сонгож авч болохгүй. Физик утга учир нь 5.3 – т тайлбарлагдах болно.
Дээр хоёр өөр төрлийн жишээний үр дүнг зураг 5.1 – ээр харуулав. Өгөгдөл нь 4.2 жишээнийхтэй ижил. Эхний тохиолдол нь alpha=0.9 болон хугацааны алхам нь delta t=500s байхаар авсан. Тэгээд sigma=0.5 хүртэлх утганд тогтворшилтын нөхцөл хангагдаж байна. Энэ нь 5.1а зургаар батлагдаж байгаа ба тэнд график нь нилээд гөлгөр харагдаж байна. Хоёр дахь жишээнд хугацааны алхамыг 1000с хүртэл ихэсгэж sigma=1 тэй болоход тогтворшилтын нөхцөл зөрчигдөж байна. 5.2b зурганд шийдэл тогтворжилтгүй байна. 4.2 хэсэгт байсан жишээнд alpha=0 байсан ба энэ нь ямарч хугацааны алхамтай байсан тогтворгүй байжээ. Өмнөх нийтлэлийн Figure 1 гэдгийг үзээрэй.
Үүнд sigma=u*delta t/delta x ба psi=2*pi*delta x/L байна. Хамгийн бага байх боломжит торны хэмжээ мэдээж delta x=0 байх юм. Өөрөөр хэлбэл, Хамгийн их байх боломжит утга нь delta x=L/2 байх ба долгионы уртад хоёроос доош цэгтэй тор хэрэглэж долгионыг харуулна гэдэг байж болошгүй юм. Эсрэгээр, Хамгийн бага боломжит долгионы урт нь 2delta x гэсэн тодорхой торны цэгүүдэд л дүрслэгдэх болно. За ямарч байсан үр дүн нь дараах байдалтай байна.
Харин тогтворжилтын шаардлага нь тэгшитгэл 5.3-д байх бүх л утгын хувьд:
Аятайхан байдлаар 5.4 тэгшитгэлийг сийрүүлбэл
Энэ бол cos psi – ийн шугаман функ байна. Тэгэхээр хэрэв ялгаатай байдал нь хоёр туйлын утга болох +-1 утганд хангалттай байвал энэ нь дундаж утгатай гэсэн үг. Үүнийг бичвэл
Засварласан Лакс-ийн схемд тогтворшилтын нөхцлөөр дээрх хоёрыг нэгтгэн бичвэл:
Үүний утга нь бид alpha болон delta x – ийг сонгож дараа нь 5.5 тэгшитгэлээр хязгаарлагдсан delta t – г сонгож болно гэсэн үг юм. Хугацааны алхамыг дурын байдлаар сонгож авч болохгүй. Физик утга учир нь 5.3 – т тайлбарлагдах болно.
Дээр хоёр өөр төрлийн жишээний үр дүнг зураг 5.1 – ээр харуулав. Өгөгдөл нь 4.2 жишээнийхтэй ижил. Эхний тохиолдол нь alpha=0.9 болон хугацааны алхам нь delta t=500s байхаар авсан. Тэгээд sigma=0.5 хүртэлх утганд тогтворшилтын нөхцөл хангагдаж байна. Энэ нь 5.1а зургаар батлагдаж байгаа ба тэнд график нь нилээд гөлгөр харагдаж байна. Хоёр дахь жишээнд хугацааны алхамыг 1000с хүртэл ихэсгэж sigma=1 тэй болоход тогтворшилтын нөхцөл зөрчигдөж байна. 5.2b зурганд шийдэл тогтворжилтгүй байна. 4.2 хэсэгт байсан жишээнд alpha=0 байсан ба энэ нь ямарч хугацааны алхамтай байсан тогтворгүй байжээ. Өмнөх нийтлэлийн Figure 1 гэдгийг үзээрэй.
Одоо энэ хоёр түвшний гэгдэх аргаар бодсон жишээг авч
үзье.
!
Computational hydraulics Section 5
! water
quality in Lake
! pp.23 eq(5.1)
! two
level method
parameter(nx=100,dx=1.0) ! [m]
parameter(nt=1000,dt=1) ! time [sec]
parameter(u=0.5) ! Velocity [m/sec]
dimension c1(nx),c2(nx)
open(10,file='result7.dat') !file open
do j=1,nx
c1(j)=0.0 !
initial value
if(j.gt.3.and.j.lt.20) c1(j)=1.0 !
initial value
enddo
write(*,*) "alpha"
read(*,*)alpha
do n=1,nt ! temporal change
do j=2,nx-1
rh=-u*(c1(j+1)-c1(j-1))/(2*dx)
c2(j)=rh*dt+0.5*alpha*(c1(j+1)+c1(j-1))+(1-alpha)*c1(j)
enddo
c1=c2
write(10,'(1000f7.2)') (c1(j),j=1,nx)
!output
enddo
close(10) !file close
stop
end
Figure 2. alpha=1 гэж өгсөн үеийн шийдэл
Програмчлалд write(*,*)
"alpha"
read(*,*)alpha гэсэн 2 мөр нь alpha
– гийн
утгыг гарнаас өгөх боломж олгож байгаа юм. Тэгээд гарнаас өгөхөд дээрх 2 үр
дүнг харж болно. 2 дахь нь гөлгөр болох шахсан байгаа. Гэхдээ үл ялиг барзгар
шаталсан байгаа нь бүхэлдээ шийдэл тогтворгүй гэж хэлэхэд хэцүү. Энэ хоёр
шийдлийн хугацааны алхам нь deltha
t=0.1с байхаар маш бага өгсөн учраас номны жишээтэй адил маш
барзгар гарах боломжгүй.
Хоёр
түвшний гэж нэрлэгдэх болсон нэрний хувьд жаахан тайлбар өгье. 5.1 тэгшитгэлийг
ажиглавал j – ийн дараалсан 3 –
н утга байж гэмээн n+1 утгыг
бодож болохоор харагдаж байна.
Figure 3. Төгсгөлөг ялгаварын торны схем
Figure 3. Төгсгөлөг ялгаварын торны схем
n – ийн
утгыг мэдэж байхад n+1
– ийг тодорхойлно. Дараагын хугацааны алхамд саяны тодорхойлсон n+1 нь n болох ёстой.
Нэг хоёр, хоёр тэнцүү нэг, нэг хоёр гэх мэтээр тодорхойлж байгаа учир хоёр
түвшний арга гэж нэрлэж байгаа юм.
5.2 Мэлхий үсрэлтийн арга /Leap-Frog
method/
Хугацаа ба орон зайн гаргалгаа нь ухрах
ялгавар болон төвийн ялгаварын гэсэн ялгаатай байдлаар шийдвэрлэгдсэн гэдгийг
тэмдэглэе. Хугацааны гаргалгааг төвийн ялгаварын аргаар ойролцоолбол мэлхий
үсрэлтийн аргыг өгнө.
Нэрний учир нь энэ тэгшитгэлд хэрэглэсэн торны цэгүүдийн хэв маягыг авч үзвэл ойлгогдох болно. Энэ бол гурван түвшний арга юм. Хэрэв 2 хугацааны түвшин мэдэгдэж байвал гуравдах нь нарийн тодорхойлогдох болно (цэг цэгээр гэх мэт). Хэдий тийм боловч, t=0 үед зөвхөн нэг анхны нөхцөл өгөгдсөн бол мэлхий үсрэлтийн аргыг хэрэглэх боломжгүй болно. Бид n=1 түвшинд хоёр түвшний (Засварласан Лаксын арга) аргыг хэрэглэн тоон шийдлийг эхлүүлэх хэрэгтэй болно. Доод хашицын хязгаарт, 5.6 тэгшитгэлийн дээд хэсгийн хувилбар хэрэглэгдэнэ.
Нэрний учир нь энэ тэгшитгэлд хэрэглэсэн торны цэгүүдийн хэв маягыг авч үзвэл ойлгогдох болно. Энэ бол гурван түвшний арга юм. Хэрэв 2 хугацааны түвшин мэдэгдэж байвал гуравдах нь нарийн тодорхойлогдох болно (цэг цэгээр гэх мэт). Хэдий тийм боловч, t=0 үед зөвхөн нэг анхны нөхцөл өгөгдсөн бол мэлхий үсрэлтийн аргыг хэрэглэх боломжгүй болно. Бид n=1 түвшинд хоёр түвшний (Засварласан Лаксын арга) аргыг хэрэглэн тоон шийдлийг эхлүүлэх хэрэгтэй болно. Доод хашицын хязгаарт, 5.6 тэгшитгэлийн дээд хэсгийн хувилбар хэрэглэгдэнэ.
Тогтворшилтыг өмнөхтэй адил байдлаар авч
үзвэл
Тэгшитгэл 5.6 – д энэ тэгшитгэлийг танилцуулж ердийн хүчин зүйлээр хуваахад нэмэгдэлтийн хүчин зүйлийн квадрат тэгшитгэлийг өгнө.
Энэ тэгшитгэл дараах хоёр язгууртай байх болно.
Вон Неуманны дараах нөхцөл биелж байхад үүнийг батлан харуулах нь хэцүү биш.
Хэрэв |sigma|=1 бол тогтворшилтын хязгаар дээр шийдэл орших ба хуваарилалт өсөхгүй, унтрасаар байх болно. Харахад, ижил долгионы урттай хоёр тоон шийдэл байх ба нэг нь физик шийдэлтэй, нөгөө нь хуурмаг эсвэл тоон бүрдүүлэгчтэй тохирч байна. Сүүлчийх нь боломжтой бага юм шиг хадгалагдах хэрэгтэй. 5.9 – д байх тогтворшилтын нөхцөл засварласан Лаксын аргаас тийм ч өөр биш боловч мэлхий үсрэлтийн арга нь илүү нарийвчлалыг үзүүлдэг. (5.4 хэсэг)
Тэгшитгэл 5.6 – д энэ тэгшитгэлийг танилцуулж ердийн хүчин зүйлээр хуваахад нэмэгдэлтийн хүчин зүйлийн квадрат тэгшитгэлийг өгнө.
Энэ тэгшитгэл дараах хоёр язгууртай байх болно.
Вон Неуманны дараах нөхцөл биелж байхад үүнийг батлан харуулах нь хэцүү биш.
Хэрэв |sigma|=1 бол тогтворшилтын хязгаар дээр шийдэл орших ба хуваарилалт өсөхгүй, унтрасаар байх болно. Харахад, ижил долгионы урттай хоёр тоон шийдэл байх ба нэг нь физик шийдэлтэй, нөгөө нь хуурмаг эсвэл тоон бүрдүүлэгчтэй тохирч байна. Сүүлчийх нь боломжтой бага юм шиг хадгалагдах хэрэгтэй. 5.9 – д байх тогтворшилтын нөхцөл засварласан Лаксын аргаас тийм ч өөр биш боловч мэлхий үсрэлтийн арга нь илүү нарийвчлалыг үзүүлдэг. (5.4 хэсэг)
!
Computational hydraulics Section 4
! water
quality in Lake
! pp.20
eq(5.6)
!
Leap-frog method
parameter(nx=100,dx=1.0) ! [m]
parameter(nt=1000,dt=0.1) ! time [sec]
parameter(u=0.5) ! Velocity [m/sec]
dimension c1(nx),c2(nx),c3(nx)
open(10,file='result_7.dat') !file open
do j=1,nx
c1(j)=0.0 !
initial value
if(j.gt.3.and.j.lt.20) c1(j)=1.0 !
initial value
enddo
do n=1,nt ! temporal change
do j=2,nx-1
ra=-u*(c1(j+1)-c1(j-1))/(2*dx)
c2(j)=ra*dt+c1(j)
enddo
! c1=c2 ! 2015 оны 1 сарын 31нд алдааг олж засав
do j=3,nx-1
rh=-u*(c2(j+1)-c2(j-1))/(2*dx)
c3(j)=rh*2*dt+c1(j)
enddo
c1=c2
c2=c3
write(10,'(1000f7.2)') (c1(j),j=3,nx)
!output
enddo
close(10) !file close
stop
end
Алдаатай бодолтын хариу. Захын нөхцлийг буруу интеграцид байрлуулсан байв.
Захын нөхцлийг зөв байрлуулсаны дараах үр дүн. 2015/1/31 оны засварыг хийснээр энэ үр дүнг авав.
5.3 CFL нөхцөл
Тогтворшилтын шинжилгээнд хэмжээсгүй тоог
ажигласан байх, энэ тоо чухал үүрэг гүйцэтгэнэ.
Үүнийг Коурантийн тоо гэх ба 5.9 нөхцлийг CFL (Courant-Friedrichs-Lewy condition) гэж анх математикт тэмдэглэжээ. Характеристикийн онолтой холбогдсон бага гэлтгүй тайлбар 4.1 хэсэгт дурьдагдсан байгаа. Зураг 5.2 – т засварлагдсан Лаксийн арга дүрслэгдсэн байна.
Үүнийг Коурантийн тоо гэх ба 5.9 нөхцлийг CFL (Courant-Friedrichs-Lewy condition) гэж анх математикт тэмдэглэжээ. Характеристикийн онолтой холбогдсон бага гэлтгүй тайлбар 4.1 хэсэгт дурьдагдсан байгаа. Зураг 5.2 – т засварлагдсан Лаксийн арга дүрслэгдсэн байна.
Хэрэв xj
цэг дэх концентрацийг ажиглавал бид характеристикийн хурд u – гаар
дамжуулагдах концентрацыг харж болно. Хугацаа tn+1 үед, цэгийн
дундуур гарсан характеристикийн доод хэсэгт бүсийн нөлөөлөл байх ба үүнийг
нөлөөллийн бүс гэж нэрлэнэ. Характеристикийн дээд хэсэгт байгаа бүхэн чухал
биш.
Тооцон бодох аргад, (j,n+1)
утга нь гурван суурь цэгээр тодорхойлогдоно. Хэрэв sigma<1 болбол (Зураг 5.2а) гурван цэг
нь нөлөөллийн бүсэд багтана. Өөрөөр хэлбэл А цэг нөлөөллийн бүсэд багтаж байх
иймэрхүү нөхцөлтэй байхад илүү тогтворжилттой шийдлийг авах болно. Нөгөө
тохиолдол болох sigma
>1 бол (Зураг
5.2b) суурь
цэгүүд нөлөөллийн бүсэд багтахгүй болох ба энэ нөхцлөөр шийдлийг гарган авч
болох боловч физик утгын хувьд боломжгүй, шийдэл буруу буюу тогтворгүй байна.
Өөр байдлаар тайлбарлаж болно. (j,n+1)
цэг дахь концентрацийг А цэгийн тусламжтай тодорхойлно гэе. Тэгвэл А цэг
торын цэгүүдийн дунд интерполяцлагдаж (Зураг
5.2а) байвал
асуудалгүй, харин эксртаполяцлагдаж
(Зураг 5.2b) байвал
тогтворгүй байдалруу уриалах болно.
Тооцон бодогч хэн бүхэн CFL нөхцөл чухал гэдгийг мэдэж байх хэрэгтэй боловч энэ нь тийм ч хангалттай биш юм.
Тооцон бодогч хэн бүхэн CFL нөхцөл чухал гэдгийг мэдэж байх хэрэгтэй боловч энэ нь тийм ч хангалттай биш юм.
5.4 Хасалтын алдаа /Truncation
Error/
Тогворжилттой төгсгөлөг ялгаварын аргаар нарийвчилсан үр
дүнг тэр болгон авч чадахгүй тохиолдол байна. Нарийвчлалыг судлах хоёр янзын
арга байдаг ба үүний нэг нь хасалтын алдааны хэмжээг тодорхойлох явдал юм. Хэрэв
дифференциал тэгшитгэлийн шийдлийг ялгаварын тэгшитгэлд орлуулж дахин
дифференциал тэгшитгэл гарган авах боломжгүй. Зарим тохиолдолд гаргаж авч болох
ч их ховор. Үүнийг суурь цэгтэй (ихэнх
тохиолдолд j,n цэгийг
авна)
холбогдсон Тэйлорын цуваанаас шийдлийг гарган авах процессоос харж болно.
Ингээд хоёр хэмжээст Тэйлорын цувааг авч үзье.
Эдгээрийг 4.9 тэгшитгэлд орлуулж, хоёр ба түүнээс дээших эрэмбийн илэрхийллийг тооцолгүйгээр бичвэл
Зүүн гар талых нь дифференциал тэгшитгэл гэдгийг мэднэ. Харин баруун талых нь 0 байх ёстой бөгөөд үүнийг л хасалтын алдаа гэж нэрлэж байгаа юм. Энэ бол шийдлийн алдаа бус тэгшитгэлийн алдаа гэдгийг санаж байх хэрэгтэй. Тэгшитгэл 5.10 нь бидний өмнө шийдвэрлэсэн тэгшитгэлийн засварлаагүй хэлбэр юм. Хасалтын алдаа нь илэрхийлэлд delta t болон delta x – ийн харьцааны нэг зэрэгт хэлбэртэй байгаа учир засварласан Лаксийн арга нь нэгдүгээр эрэмбийнх болж байна. Хэрэв delta t delta x нь хангалттай бага бол алдаа бага байна. Гэхдээ хэр бага байх вэ гэдэг нь асуудал юм. Энэ нь тооцож буй проблемийн хугацаа болон орон зайн хүрээнээс хамааралтай байна. Долгионы шилжилтийн авч үзье.
Энд w=uk байх ба тэгшитгэл 5.10 – ийн дөрвөн илэрхийллийн хоорондын харьцаа:
Хасалтын алдааг бага байлгахын тул дараах нөхцлүүдийг авна.
Эдгээр нь хэрэглэж болохуйц delta t, delta x – ийн утгыг ойролцоолох боломж олгодог. Гэсэн хэдий ч практикт үүнийг ашиглах нь зарим үед хүндрэлтэй байх ба хасалтын алдаа нь шийдэлд хэрхэн нөлөөлж байгааг тодорхойлоход бэрхшээлтэй болдог.
Эдгээрийг 4.9 тэгшитгэлд орлуулж, хоёр ба түүнээс дээших эрэмбийн илэрхийллийг тооцолгүйгээр бичвэл
Зүүн гар талых нь дифференциал тэгшитгэл гэдгийг мэднэ. Харин баруун талых нь 0 байх ёстой бөгөөд үүнийг л хасалтын алдаа гэж нэрлэж байгаа юм. Энэ бол шийдлийн алдаа бус тэгшитгэлийн алдаа гэдгийг санаж байх хэрэгтэй. Тэгшитгэл 5.10 нь бидний өмнө шийдвэрлэсэн тэгшитгэлийн засварлаагүй хэлбэр юм. Хасалтын алдаа нь илэрхийлэлд delta t болон delta x – ийн харьцааны нэг зэрэгт хэлбэртэй байгаа учир засварласан Лаксийн арга нь нэгдүгээр эрэмбийнх болж байна. Хэрэв delta t delta x нь хангалттай бага бол алдаа бага байна. Гэхдээ хэр бага байх вэ гэдэг нь асуудал юм. Энэ нь тооцож буй проблемийн хугацаа болон орон зайн хүрээнээс хамааралтай байна. Долгионы шилжилтийн авч үзье.
Энд w=uk байх ба тэгшитгэл 5.10 – ийн дөрвөн илэрхийллийн хоорондын харьцаа:
Хасалтын алдааг бага байлгахын тул дараах нөхцлүүдийг авна.
Эдгээр нь хэрэглэж болохуйц delta t, delta x – ийн утгыг ойролцоолох боломж олгодог. Гэсэн хэдий ч практикт үүнийг ашиглах нь зарим үед хүндрэлтэй байх ба хасалтын алдаа нь шийдэлд хэрхэн нөлөөлж байгааг тодорхойлоход бэрхшээлтэй болдог.
5.5 Долгионы тархалт /Wave
propagation/
Төгсгөлөг ялгаварын шийдлийн нарийвчлалыг судлах хоёр
дахь арга бол Вон Неуманны шинжилгээ юм. Энд авч үзэж буй энгийн тохиолдолд, дифференциал
болон төгсгөлөг ялгаварын тэгшитгэлийн аналитик шийдлүүд хоорондоо
харьцуулагдах болно. Энэ нь илүү төвөгтэй нөхцөлд үр дүнтэй байх шинж чанарыг
үзүүлнэ. Анхны нөхцлийг дахин авч үзье.
Тасралтгүй тохиолдолд аналитик шийдэл нь:
Вон Неуманны шинжилгээнээс, төгсгөлөг ялгаварын шийдэл нь
Энд Ф нь нэмэгдэлтийн хүчин зүйлийн (ro) аргумент юм. 5.14 болон 5.15 тэгшитгэлд байгаа хэлбэлзлүүдийн харьцаа нь дараагын n алхам дахь бууралтын хүчин зүйлийг илтгэнэ.
Фазын өнцөг эсвэл тархалтын хурдны харьцаа нь
Тасралтгүй тохиолдолд аналитик шийдэл нь:
Вон Неуманны шинжилгээнээс, төгсгөлөг ялгаварын шийдэл нь
Энд Ф нь нэмэгдэлтийн хүчин зүйлийн (ro) аргумент юм. 5.14 болон 5.15 тэгшитгэлд байгаа хэлбэлзлүүдийн харьцаа нь дараагын n алхам дахь бууралтын хүчин зүйлийг илтгэнэ.
Фазын өнцөг эсвэл тархалтын хурдны харьцаа нь
Өмнөх бүлэг Ууссан бодисын тээвэрлэлт



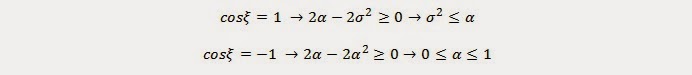












No comments:
Post a Comment