Ууссан бодисын тээвэрлэлт /Transport of Dissolved substance in River/

Бүлэг 4

Ууссан бодисын тээвэрлэлт

4.1 Математик илэрхийлэл

Тодорхой хэмжээтэй бодис голруу цутгаж байгаа гэж үзье тэгвэл голын уртын дагууд хэрхэн тээвэрлэгдэх бол? Цаг хугацааны турш тархалтыг /diffusion/ үл тооцож болно. Тэгэхээр бодит биш болох боловч дараах бүлгүүдэд үүний тухай авч үзэх болно. Үр дүн нь бодис цутгагдаж байгаа зарцуулгын хамт голын уртын дагууд тээвэрлэгдэх болно (зураг 4.1). Хэрэв зарцуулга dt хугацаа явбал бөөн зарцуулгын урт нь dt*u болно. Энд u нь урсгалын дундаж хурд болно. t хугацааны дараа бүхэл зарцуулга ut зайнд тээвэрлэгдсэн байх болно. Гол хугацаанд бодис нь Бүлэг 2 – т үзсэн шиг тайвшралтын хугацаагаар задарч болох юм. Үнэндээ урсгалын хурдаар тээвэрлэгдэж байгаа бүхэл зарцуулгын хувьд өмнөх бүлэгтэй ижил томъёоллыг хэрэглэж болох юм. Гэхдээ энэ хандлага нь илүү хүндэвтэр тохиолдлыг хялбархан дүгнэж чадахгүй. Тиймээс delta x уртын дагууд голын хөндлөн огтлол А – гаар хүрээлэгдсэн элемантар хяналтын эзлэхүүний хувьд массын балансыг авч үзэх нь илүү дээр болж байна.

Адил хяналтын эзлэхүүн дахь усны балансыг ижил байдлаар авч үзвэл үр дүн нь:

Энд Q бол усны зарцуулга.

 

4.1 тэгшитгэлд хувиргалт хийн 4.2 тэгшитгэлийг ашигласанаар дараах тэгшитгэлийг гаргах боломжтой.

Ийм төрлийн тэгшитгэл физикийн маш олон хэрэглээнд тааралддаг. Үүнийг энгийн долгионы тэгшитгэл гэж нэрлэх болсоныг доор тайлбарлая. Харин сүүлийн илэрхийлэл байхгүй бол advection тэгшитгэл гэж нэрлэдэг.

Хэрэв ямарч задралгүй (Т нь хязгааргүй рүү тэмүүлж байвал) шийдлийн шинж чанар нь маш ойлгомжтой байдлаар дүрслэгдэнэ. Тэгээд тэгшитгэл 4.3 нь хяналтын эзлэхүүн дахь бохирдлын концентраци тогтмол болохыг харуулна. Хэрвээ та ажиглагч болоод усны хяналтын эзлэхүүнтэй цуг хөдөлбөл (delta x/delta t=u хурдтай) концентраци тогтмол байгааг харах болно (зураг 4.3а).  Концентрацийн утга нь замын эхлэл хэсэгт байсан шиг л уртын дагууд шилжих болно. Хэрэв зарцуулгын цэг нь доод хашицад t=0 хугацаанд байсан бол тэнд концентраци ямар байхыг мэдэх хэрэгтэй. Тиймээс t=0 хугацаанд тухайн мужын цэг бүрийн анхны нөхцөл хэрэгтэй болно. Хэрэв чиглэл t>0 зарцуулгын цэгээс эхлэвэл бас л хязгаарын нөхцөл болох концентрацийг мэдэх хэрэгтэй болно. Энэ тохиолдолд зарцуулгын цэг дахь концентрацыг масс балансын тэгшитгэлээс дахин тодорхойлж болно. Хэрэв зарцуулга байхгүй бас жинхэнэ концентраци тэг бол доод хашицад байх Qс хольцын массын урсгал нь нийт зарцуулалт F(t) – тэй тэнцүү байх хэрэгтэй.

Тэгэхээр,

Энд том голуудын хувьд бодитой биш ч гэсэн зарцуулгын цэг дээр бүрэн холигдсон гэдэг нөхцлийг авч үзсэнээр гарч ирнэ.

Хэрэв тэнд задрал (Т төгсгөлөг, Зураг 4.3b харах) байх юм бол нөхцөл байдал ижил байна. Усны урсгалтай хамт хөдөлж байгаа ажиглагч тогтмол концентрацыг олж харахгүй, гэвч задрал бүр тайвшрах хугацааг (T) агуулсан e функцаар буурна. Анхны болон хязгаарын нөхцөлийн үр дүн нь ижил болно. Чиглэлийн дагуу, буюу урсгалын дагуу концентраци эхний тохиолдолд тогтмол, хоёр дахь нөхцөлд e функцаар буурч байгаа энэ үзэгдлийг характеристик (Физикт элбэг тохиолдох ба функцийн характеристик гэж нэрлэх нь бий.) гэнэ. Энэ тохиолдолд характеристик цэг (x,t) бүрийн дагуу өнгөрөх ба энэ нь усны бүхэл хэсгийн замтай давхцаж байна.

Дараагаар бусад төрлийн характеристикууд тааралдах болно. Характеристик нь шийдлийн шинж чанар зарим характеристикийг харуулдаг (тиймээс нэр нь учиртай). Манай жишээнд байгаа төрлийн шийдэл нь характиристик хурд u – гаар хөдөлж байгаа “энгийн” давалгаа бөгөөд унтарч байгаа эсвэл тогтмол байгаа онцлогтой юм.

Хэрэв цэг бүрийн характеристикийн тоо нь тухайн дифференциал тэгшитгэлийн эрэмбэтэй тэнцүү бол энэ системийг гиперболлог (hyperbolic) систем гэнэ. Дараа бид параболик болон элипслэг тохиолдолуудтай таарна. Ихэвчлэн, гиперболлог тэгшитгэл нь долгион \давалгаа\ үзэгдэлтэй холбоотой асуудлыг шийдэхэд тохиолдоно.

4.2 Тоон шийдэл /Numerical solution/

Энгийн долгионы тэгшитгэл (4.3) – ийг салангад байдлаар тоон аргаар шийдвэрлэнэ. Одоо зөвхөн хугацааны алхам delta t танилцуулагдахгүй, delta x хэмжээтэй торон доторхи салангид зай орж ирнэ. (Зураг 4.5) n*delta t хугацаа болон j*delta x байрлал дахь концентрацын утга cj(n)   – ээр тэмдэглэгдэнэ. Хугацаа оршин байхад, u=const гэж үзвэл ямарч задрал байхгүй болно.

Цэг ( ) дээрхи төгсгөлөг ялгавараар ойролцоолбол тухайн гаргалгаанууд нь дараах байдалтай байна.

Дээрх хоёулаа “салхины эсрэг” (upwind scheme) ялгаварууд байна. Орон зайн гаргалгааны хувьд “төвийн ялгавар” (central scheme) – ын аргыг хэрэглэх нь нарийвчлалын хувьд өндөр байх талтай.

Тэгшитгэл 4.6 болон 4.8 – ийг нэгтгэвэл дараах ялгаварын тэгшитгэлийг өгнө.

Эсвэл 

t=0 (n=0) үе дахь торны бүх цэгүүдийн анхны утга өгөгдсөн үед j=0 болон j=J хязгаарын цэгүүдийн торны бүх цэгүүд дахь t=delta t (n=1) хугацаанд утгуудыг тооцоолох боломжтой болно. Энэ хэлбэрт, хязгаарын нөхцөл өгөгдсөн байна. Хязгаарт j=J, энэ нь хуурмаг нэг бөгөөд тэгшитгэл 4.10 – д бүсээс гаднах цэгийг шаардах учир хэрэглэх боломжгүй. Иймд “ухрах” ялгаварын (backward scheme) аргыг хэрэглэн тэгшитгэл 4.10 – ийн өөр нэг хэлбэрийг бичиж болно.

Энэ замаар n=1 түвшин дахь бүхэл хугацааг тооцоолж болно. Тэгээд үйлдэл дараагын хугацааны түвшинд давтагдах ба шаардлагатай хугацаа хүртэл явна. Концентрацийн шинэ утга бүр хугацааны түвшин дахь утгаас нарийн тооцологдоно. Энэ бол “ил” гэж нэрлэгдэх төгсгөлөг ялгаварын схемийн (explicit finite difference schemes) төрөл юм.

Аналитик шийдэл болон тоон шийдлийг цугт нь агуулсан жишээ зураг 4.6 – д өгөгдөв. Энэ нь өмнөх хэсгээс характеристикийн теоромыг ашиглан хялбархан тодорхойлогдох болно.

Нөхцөл байдал нь хадгалагдах хольцын (задралгүй, яг давс шиг) зарцуулга t=0 хугацаанд x=0 эхлэлийн цэгт тасралтгүй байна. Зарцуулгын цэгийн доод хэсгийн концентраци нь c_o гэж нэрлэгдсэн. Урсгалын хурд u=0.5м/с байна. 3 цагийн дараа давс нь голын уртын дагуу 5 км орчимд тархсан байна. Тооцоонд диффузи байхгүй учир урд хэсгийн хэлбэр нь хурц хэлбэртэй байна. Тооцоолох параметр нь delta x=500м, ба delta t=500с байна. Харваас ямар нэгэн зүйл болохгүй банйа. Шийдлийн хэлбэлзэл муудсаар байгааг анзаарна. Үүнийг дараах байдлаар тайлбарлъя.

Дараах хэлбэрийн анхны нөхцөл байна гэж тооцъё.

Хэрвээ тэгшитгэл 4.10 – д дээрхийг танилцуулбал бүх илэрхийллүүд exp(ij psi) хүчин зүйлийг агуулах болно. Тэгэхээр 4.13 – тай ижил шинэ шийдэл гарч ирнэ.

Энд sigma=(dx/dt)*u. Тоон шийдэл нь нэмэгдэлтийн хүчин /amplification factor/ зүйл гэж нэрлэгдэх комплекс хүчин зүйлийн улмаас хугацааны алхамын турш үржигдэж байдаг.

Энэ нь хэлбэлзэл /amplitude/ нь аргумент ro – оор фаз шилжиж байгаа газар ro – оор үржигдэнэ гэсэн утгатай юм. Дараагын хугацааны алхамын үед ижил зүйл явагдана. Одоо, нэмэгдэлтийн хүчин зүйл нь psi ба sigma – ийн ямарч абсолют утганд нэгжээс илүү байна. Тэгэхээр тоон шийдлийн хэлбэлзэл нь нэмэгдэх болно. Тиймээс үүнийг тогтмол үлдээх хэрэгтэй. Үүнийг тогтворгүйжилт /instability/ гэж нэрлэнэ. Зураг 4.6 жишээнд бид анхны нөхцлөөр косинус функцыг аваагүй, гэвч өөр долгионы урттай косинус функцыг агуулсан Фурьегийн цуваанд ямар нэгэн анхны нөхцлийг гарган авч болно. Анхны нөхцөл бүр 4.15 тэгшитгэлийн дагуу гарч ирэх ба нэгдсэн нөлөөлөл нь зураг дээрх зүйл юм. Төгсгөлөг ялгаварын схем 4.10 энэ жишээний хувьд үнэндээ хэрэггүй болж байна.

Фурьегийн цувааны илэрхийлэл дахь тогтворжилтын анализ нь Вон Неюмэннээр шийдвэрлэгдсэн байна. Дараагын бүлэгт тогтворт нөхцөлд өөр өөр төгсгөлөг ялгаварын схемийг үзэх болно. Харваас, тогтворжилтын ерөнхий нөхцөл нь нэмэгдэлтийн хүчин зүйл доорхи абсолют утганд нэгжээс бага байх хэрэгтэй явдал юм.

Долгионы уртын эсвэл долгионы урт, торны хэмжээ хоёрын харьцааг агуулсан psi – ийн ямарч утганд дээрх нөхцөл хангагдах ёстой.

За ингээд энэ бүлэгт байгаа төгсгөлөг ялгаварын аргаар бичигдсэн тэгшитгэлийг хэрхэн тооцоолон бодох фортран програмыг бичье.

! Computational hydraulics Section 4

! water quality in Lake

! pp.20 eq(4.9)

! central derivertive

      parameter(nx=100,dx=1.0)  ! [m]

      parameter(nt=1000,dt=0.1) ! time [sec]

      parameter(u=0.5)          ! Velocity [m/sec]

      dimension c1(nx),c2(nx)

      open(10,file='result5.dat') !file open

      do j=1,nx

                             c1(j)=0.0 ! initial value

      if(j.gt.3.and.j.lt.20) c1(j)=1.0 ! initial value

      enddo

      do n=1,nt ! temporal change

      do j=2,nx-1

      rh=-u*(c1(j+1)-c1(j-1))/(2.*dx)    ! eq(4.9)

      c2(j)=rh*dt+c1(j)

      enddo

      c1=c2

      write(10,'(1000f7.2)') (c1(j),j=1,nx) !output

      enddo

      close(10) !file close

      stop

      end

Figure 1. Төвийн ялгаварын аргаар бодсон үр дүн

! Computational hydraulics Section 4

! water quality in Lake

! pp.20 eq(4.11)

! upwind scheme

      parameter(nx=100,dx=1.0)  ! [m]

      parameter(nt=1000,dt=0.1) ! time [sec]

      parameter(u=0.5)          ! Velocity [m/sec]

      dimension c1(nx),c2(nx)

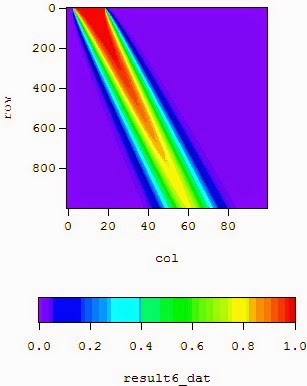
      open(10,file='result6.dat') !file open

      do j=1,nx

                             c1(j)=0.0 ! initial value

      if(j.gt.3.and.j.lt.20) c1(j)=1.0 ! initial value

      enddo

      do n=1,nt ! temporal change

      do j=2,nx-1

      rh=-u*(c1(j)-c1(j-1))/dx        ! eq(4.11)

      c2(j)=rh*dt+c1(j)

      enddo

      c1=c2

      write(10,'(1000f7.2)') (c1(j),j=1,nx) !output

      enddo

      close(10) !file close

      stop

      end

Figure 2. Салхины эсрэг ялгаварын аргаар тооцсон үр дүн.